ndarray 객체 구조, 고급 배열 조작 기법, 브로드캐스팅, 고급 ufunc 사용법

ndarray 객체 구조

NumPy의 ndarray는 연속적이든 아니든 단일 형태의 데이터 블록을 다차원 배열 객체 형태로 해석할 수 있는 수단을 제공한다. dtype이라고 하는 자료형은 데이터가 실수, 정수, 불리언 혹은 다른 형인지 알려주는 역할을 한다.

ndarray는 모든 배열 객체가 띄엄띄엄 떨어진 데이터 블록에 대한 뷰^view라서 유연하다. 예를 들어 arr[::2, ::-1] 배열이 데이터 복사가 일어나지 않는 이유는 ndarray가 단순한 메모리 덩어리와 dtype만 가지는 것이 아니기 때문이다. 좀 더 설명하자면, ndarray는 내부적으로 다음과 같이 구성되어 있다.

• 데이터 포인터: RAM이나 메모리 맵 파일에서 데이터의 블록

• dtype은 배열 내에서 값을 담는 고정된 크기를 나타낸다. ex) 4바이트, 8바이트

• 배열의 모양(Shape)을 알려주는 튜플

• 하나의 차원을 따라 다음 원소로 몇 바이트 이동해야 하는지를 나타내는 stride를 담고 있는 튜플

예를 들어 10x5 크기의 배열의 모양은 (10, 5)로 표현된다.

np.ones((10, 5)).shape

(10, 5)

C언어 형식의 3x4x5 크기의 float64(8바이트) 배열은 (160, 40, 8)의 stride 값을 가진다. 일반적으로 stride 값이 클수록 해당 축을 따라 연산을 수행하는 비용이 많이 들기 때문에 stride 정보를 알고 있으면 편리하다.

stride 값에서 (160, 40, 8)의 의미는 160 = 4 x 5 x 8, 40 = 5 x 8, 8은 8바이트를 의미한다.

np.ones((3, 4, 5), dtype=np.float64).strides

(160, 40, 8)

stride 값은 복사가 이루어지지 않는 배열의 뷰를 생성하는 데 중요한 역할을 한다. stride 값은 음수일 수도 있는데 이는 메모리상에서 뒤로 이동해야 한다는 의미다. 배열을 obj[::-1] 또는 obj[:, ::-1] 형태로 잘라내는 경우가 그렇다.

NumPy dtype 구조

종종 배열에 담긴 값이 정수, 실수, 문자열 혹은 파이썬 객체인지 확인하는 코드를 작성할 경우가 있다. dtype은 np.issubdtype 함수와 결합하여 사용할 수 있는 np.integer나 np.floating같은 부모 클래스를 가진다.

ints = np.ones(10, dtype=np.uint16)

floats = np.ones(10, dtype=np.float32)

np.issubdtype(ints.dtype, np.integer)

True

np.issubdtype(floats.dtype, np.floating)

True

특정 dtype의 모든 부모 클래스는 mro 메서드를 이용해서 확인할 수 있다. 여기서 MRO는 Method Resolution Order로 자식과 부모 클래스를 전부 포함하여 메서드의 실행 순서를 지정하는 것이다.

np.float64.mro()

[numpy.float64,
 numpy.floating,
 numpy.inexact,
 numpy.number,
 numpy.generic,
 float,
 object]

따라서 아래와 같이 ints가 np.number 형임을 확인할 수 있다.

np.issubdtype(ints.dtype, np.number)

True

고급 배열 조작 기법

배열을 세련된 방법으로 색인하고, 나누고, 불리언 값의 일부를 취하는 다양한 방법이 존재한다.

배열 재형성하기

배열의 모양을 변환하려면 배열의 인스턴스 메서드인 reshape 메서드에 새로운 모양을 나타내는 튜플을 넘기면 된다.

arr = np.arange(8)

print('arr:', arr)
print('arr.shape:', arr.shape)

arr: [0 1 2 3 4 5 6 7]
arr.shape: (8,)

re_arr = arr.reshape((4, 2))

print('re_arr:\n', re_arr)
print('re_arr.shape:', re_arr.shape)

re_arr:
 [[0 1]
 [2 3]
 [4 5]
 [6 7]]
re_arr.shape: (4, 2)

order 인자에 주는 값에 따라 우선 순위를 정할 수 있는데 order=’C’는 로우를, order=’F’는 칼럼을 우선으로 재형성할 수 있다.

# C 순서(로우 우선)
arr.reshape((4, 2), order='C')

array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7]])

# 포트란 순서(칼럼 우선)
arr.reshape((4, 2), order='F')

array([[0, 4],
       [1, 5],
       [2, 6],
       [3, 7]])

다차원 배열 또한 재형성이 가능하다.

arr.reshape((4, 2)).reshape((2, 4))

array([[0, 1, 2, 3],
       [4, 5, 6, 7]])

reshape에 넘기는 값 중 하나가 -1이 될 수도 있는데 이 경우에는 원본 데이터를 참조해서 적절한 값을 추론하게 된다.

arr = np.arange(15)

arr.reshape((5, -1)) # arr.reshape((5, 3)) 으로 추론

array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11],
       [12, 13, 14]])

배열의 shape 속성은 튜플이므로 reshape 메서드에 이를 직접 넘기는 것도 가능하다.

other_arr = np.ones((3, 5))

other_arr.shape

(3, 5)

arr.reshape(other_arr.shape) # shape: (15,) -> (3, 5)

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

다차원 배열을 낮은 차원으로 변환하는 것을 평탄화^{flattening, raveling}라고 한다.

arr = np.arange(15).reshape((5, 3))

print('arr:\n', arr)
print('arr.shape:', arr.shape)

arr:
 [[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]
 [12 13 14]]
arr.shape: (5, 3)

print('arr.ravel():', arr.ravel())
print('arr.ravel().shape:', arr.ravel().shape) # shape: (5, 3) -> (15,)

arr.ravel(): [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]
arr.ravel().shape: (15,)

ravel 메서드는 필요하지 않다면 원본 데이터의 복사본을 생성하지 않는다. flatten 메서드는 ravel 메서드와 유사하게 동작하지만 항상 데이터의 복사본을 반환한다. 즉, ravel 메서드는 복사본이 아닌 참조본이고 flatten메서드는 복사본이다.

print('arr.flatten():', arr.flatten())
print('arr.flatten().shape:', arr.flatten().shape) # shape: (5, 3) -> (15,)

arr.flatten(): [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14]
arr.flatten().shape: (15,)

다음은 같은 같은 코드지만 ravel과 flatten의 차이를 나타낸 것이다.

arr = np.arange(8)
re_arr = arr.flatten()[:2]
re_arr[:] = 10

arr

array([0, 1, 2, 3, 4, 5, 6, 7])

flatten은 복사본으로 값의 변화가 없다.

arr = np.arange(8)
re_arr = arr.ravel()[:2]
re_arr[:] = 10

arr

array([10, 10,  2,  3,  4,  5,  6,  7])

ravel은 참조본으로 값의 변화가 일어났다.

C 순서와 포트란 순서

NumPy는 메모리상의 데이터 배치에 대한 유연하고 다양한 제어 기능을 제공한다. 기본적으로 NumPy 배열은 로우 우선(C) 순서로 생성된다. 즉 2차원 배열을 예로 들면 배열의 각 로우에 해당하는 데이터들은 공간적으로 인접한 메모리에 적재된다는 뜻이다. 로우 우선 순서가 아니면 칼럼 우선(포트란) 순서를 가지게 되는데 이때는 각 칼럼에 담긴 데이터들이 인접한 메모리에 적재된다.

reshape나 ravel 같은 함수는 배열에서 데이터의 순서를 나타내는 인자를 받는다.

C와 포트란 순서의 핵심적인 차이는 어느 차원부터 처리하느냐다.

• C: 로우 우선 순서
  

상위 차원을 우선 탐색한다(1번 축을 0번 축보다 우선 탐색한다).

• 포트란: 칼럼 우선 순서
  

상위 차원을 나중에 탐색한다(0번 축을 1번 축보다 우선 탐색한다).

기준축 참조 이미지

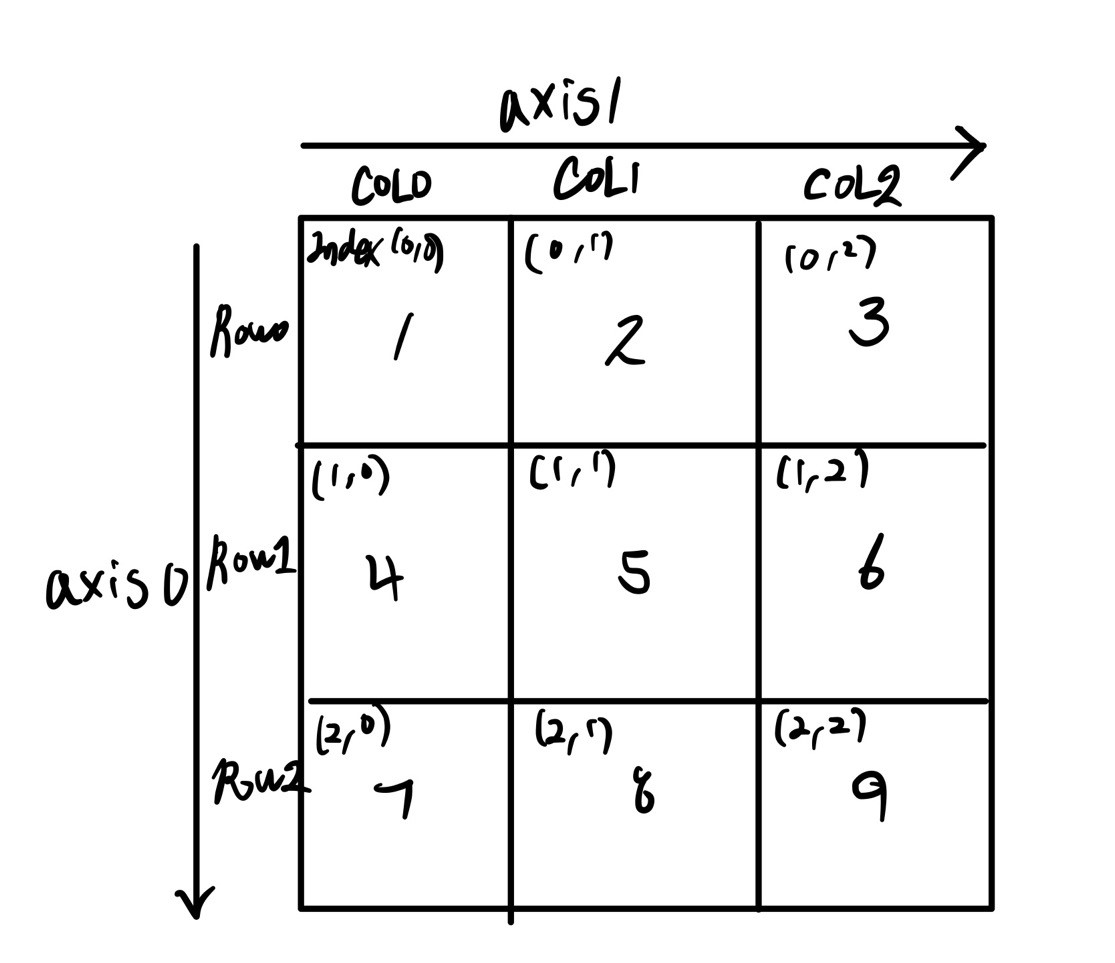
arr = np.arange(1, 10).reshape((3, 3), order='C') # order 인자의 default값은 'C'이다.

arr

array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

arr.ravel(order='C') # order 인자의 default값은 'C'이다.

array([1, 2, 3, 4, 5, 6, 7, 8, 9])

arr.ravel(order='F') # 칼럼 우선 순서로 평탄화한 모습

array([1, 4, 7, 2, 5, 8, 3, 6, 9])

배열 이어붙이고 나누기

numpy.concatenate는 배열의 목록(튜플, 리스트 등)을 받아서 주어진 축^axis에 따라 하나의 배열로 합쳐준다.

arr1 = np.array([[1, 2, 3], [4, 5, 6]]) # shape: (2, 3)
arr2 = np.array([[7, 8, 9], [10, 11, 12]]) # shape: (2, 3)

np.concatenate([arr1, arr2], axis=0) # axis=0 기준 shape: (2, 3) + (2, 3) = (4, 3) 

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

np.concatenate([arr1, arr2], axis=1) # axis=1 기준 shape: (2, 3) + (2, 3) = (2, 6)

array([[ 1,  2,  3,  7,  8,  9],
       [ 4,  5,  6, 10, 11, 12]])

vstack과 hstack함수를 이용하면 이어붙이기 작업을 쉽게 처리할 수 있다. 위 연산은 vstack과 hstack 메서드를 사용해서 다음처럼 쉽게 표현할 수 있다.

vstack은 vertical stack으로 수직(세로)로 이어붙인다고 생각하자.

np.vstack((arr1, arr2)) # axis=0

array([[ 1,  2,  3],
       [ 4,  5,  6],
       [ 7,  8,  9],
       [10, 11, 12]])

hstack은 horizontal stack으로 수평(가로)로 이어붙인다고 생각하자.

np.hstack((arr1, arr2)) # axis=1

array([[ 1,  2,  3,  7,  8,  9],
       [ 4,  5,  6, 10, 11, 12]])

split 메서드를 사용하면 하나의 배열을 축을 따라 여러 개의 배열로 나눌 수 있다.

arr = np.arange(1, 11).reshape(5, 2)

arr

array([[ 1,  2],
       [ 3,  4],
       [ 5,  6],
       [ 7,  8],
       [ 9, 10]])

first, second, third = np.split(arr, [1, 3])

전달된 값[1, 3]은 배열을 나눌 때 기준이 되는 위치인데 first, second 그리고 third는 각각 arr[:1], arr[1:3], arr[3:]을 갖는다.

print('first:\n', first) # arr[:1]
print('second:\n', second) # arr[1:3]
print('third:\n', third) # arr[3:]

first:
 [[1 2]]
second:
 [[3 4]
 [5 6]]
third:
 [[ 7  8]
 [ 9 10]]

다음은 배열을 이어붙이고 나누는 함수의 목록이다.

함수	설명
concatenate	하나의 축을 따라 배열을 이어붙인다.
vstack, row_stack	로우(axis=0)을 따라 배열을 쌓는다.
hstack	칼럼(axis=1)을 따라 배열을 쌓는다.
column_stack	hstack과 같지만 1차원 배열을 2차원 칼럼 벡터로 먼저 변환한다.
dstack	깊이(axis=2)에 따라 배열을 쌓는다.
split	특정 축을 따라 지정된 위치를 기점으로 배열을 나눈다.
hsplit, vsplit	각각 axis=0과 axis=1을 따라 배열을 나누는 함수

배열 쌓기 도우미: r_과 c_

NumPy의 네임스페이스에는 r_과 c_라는 두 가지 특수한 객체가 있는데 배열 쌓기를 좀 더 편리하게 해준다.

arr = np.arange(6)
arr1 = arr.reshape((3, 2))
arr2 = np.random.randn(3, 2)

다음은 np.concatenate([arr1, arr2], axis=0), np.vstack((arr1, arr2))와 동일하다.

np.r_[arr1, arr2]

array([[ 0.        ,  1.        ],
       [ 2.        ,  3.        ],
       [ 4.        ,  5.        ],
       [ 1.12166143, -0.11063076],
       [-0.18867534,  1.54427569],
       [ 1.57444742, -0.22065524]])

np.c_[np.r_[arr1, arr2], arr]

array([[ 0.        ,  1.        ,  0.        ],
       [ 2.        ,  3.        ,  1.        ],
       [ 4.        ,  5.        ,  2.        ],
       [ 1.12166143, -0.11063076,  3.        ],
       [-0.18867534,  1.54427569,  4.        ],
       [ 1.57444742, -0.22065524,  5.        ]])

또한 슬라이스를 배열로 변환해준다.

np.c_[1:6, -10:-5]

array([[  1, -10],
       [  2,  -9],
       [  3,  -8],
       [  4,  -7],
       [  5,  -6]])

원소 반복하기: repeat와 tile

큰 배열을 만들기 위해 배열을 반복하거나 복제하는 함수로 repeat와 tile이 있다. repeat는 한 배열의 각 원소를 원하는 만큼 복제해서 큰 배열을 생성한다.

arr = np.arange(3)

arr

array([0, 1, 2])

arr.repeat(3)

array([0, 0, 0, 1, 1, 1, 2, 2, 2])

기본적으로 정수를 넘기면 각 배열은 그 수만큼 반복된다. 만약 정수의 배열을 넘긴다면 각 원소는 배열에 잠긴 정수만크 다르게 반복될 것이다. 단 두 배열의 길이는 같아야 한다.

arr.repeat([2, 3, 4])

array([0, 0, 1, 1, 1, 2, 2, 2, 2])

다차원 배열의 경우에는 특정 축을 따라 각 원소가 반복된다.

arr = np.random.randn(2, 2)

arr

array([[-1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ]])

arr.repeat(2, axis=0) # shape: (2, 2) -> (4, 2)

array([[-1.07412104, -0.22796784],
       [-1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ],
       [ 1.45924403,  0.2787801 ]])

다차원 배열에서 만약 axis 인자를 넘기지 않으면 배열이 평탄회된다.

arr.repeat(2)

array([-1.07412104, -1.07412104, -0.22796784, -0.22796784,  1.45924403,
        1.45924403,  0.2787801 ,  0.2787801 ])

repeat 메서드에 정수의 배열을 넘기면 축을 따라 배열에서 지정한 횟수만큼 원소가 반복된다.

arr.repeat([2, 3], axis=0) # shape: (2, 2) -> (5, 2)

array([[-1.07412104, -0.22796784],
       [-1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ],
       [ 1.45924403,  0.2787801 ],
       [ 1.45924403,  0.2787801 ]])

arr.repeat([2, 3], axis=1) # shape: (2, 2) -> (2, 5)

array([[-1.07412104, -1.07412104, -0.22796784, -0.22796784, -0.22796784],
       [ 1.45924403,  1.45924403,  0.2787801 ,  0.2787801 ,  0.2787801 ]])

tile 메서드는 축을 따라 배열을 복사해서 쌓는 함수다. 타일을 이어붙이듯이 같은 내용의 배열을 이어붙인다고 생각하면 된다.

arr

array([[-1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ]])

np.tile(arr, 2) # shape: (2, 2) -> (2, 4)

array([[-1.07412104, -0.22796784, -1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ,  1.45924403,  0.2787801 ]])

tile 메서드의 두 번째 인자는 스칼라값인 타일의 개수로, 칼럼 대 칼럼이 아니라 로우 대 로우로 이어붙이게 된다. tile 메서드의 두 번째 인자는 타일을 이어붙일 모양을 나타내는 튜플이 될 수 있다.

arr

array([[-1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ]])

# 타일을 위아래로는 2개, 옆으로는 1개 놓아라!
np.tile(arr, (2, 1)) # shape: (2, 2) -> (4, 2)

array([[-1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ],
       [-1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ]])

# 타일을 위아래로는 3개, 옆으로는 2개 놓아라!
np.tile(arr, (3, 2)) # shape: (2, 2) -> (6, 4)

array([[-1.07412104, -0.22796784, -1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ,  1.45924403,  0.2787801 ],
       [-1.07412104, -0.22796784, -1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ,  1.45924403,  0.2787801 ],
       [-1.07412104, -0.22796784, -1.07412104, -0.22796784],
       [ 1.45924403,  0.2787801 ,  1.45924403,  0.2787801 ]])

팬시 인덱싱: take와 put

정수 배열을 사용한 팬시 색인 기능으로 배열의 일부 값을 지정하거나 가져올 수 있다.

arr = np.arange(10) * 100
inds = [7, 1, 2, 6]

arr[inds]

array([700, 100, 200, 600])

ndarray에는 단일 축에 대한 값을 선택할 때만 사용할 수 있는 유용한 메서드가 있다.

arr.take(inds)

array([700, 100, 200, 600])

arr.put(inds, 42) # [7, 1, 2, 6]에 해당하는 값들에 42 대입

arr 

array([  0,  42,  42, 300, 400, 500,  42,  42, 800, 900])

arr.put(inds, [40, 41, 42, 43]) # [7, 1, 2, 6]의 인덱스에 [40, 41, 42, 43] 대입

arr

array([  0,  41,  42, 300, 400, 500,  43,  40, 800, 900])

다른 축에 take 메서드를 적용하려면 axis 인자를 넘기면 된다.

inds = [2, 0, 2, 1]

arr = np.arange(1, 9).reshape((2, 4), order='F')

arr

array([[1, 3, 5, 7],
       [2, 4, 6, 8]])

arr.take(inds, axis=1)

array([[5, 1, 5, 3],
       [6, 2, 6, 4]])

put 메서드는 axis 인자를 받지 않고 평탄화된 배열(1차원, C 순서)에 대한 색인을 받는다. 따라서 다른 축에 대한 인덱싱 배열을 사용해서 배열의 원소에 값을 넣으려면 팬시 색인을 이용하는 편이 쉬울 것이다.

브로드캐스팅

브로드캐스팅은 다른 모양의 배열 간의 산술 연산을 어떻게 수행해야 하는지 설명한다. 브로드캐스팅의 가장 단순한 예제는 하나의 배열에서 스칼라값을 합칠 때 발생한다.

arr = np.arange(5)

arr

array([0, 1, 2, 3, 4])

arr * 4

array([ 0,  4,  8, 12, 16])

여기서 스칼라값 4는 곱셈 연산 과정에서 배열의 모든 원소로 브로드캐스트되었다.

예를 들어 배열의 각 칼럼에서 칼럼 평균값을 빼고 표준편차로 나눠주는 표준화를 다음처럼 간단하게 처리할 수 있다.

arr = np.random.randn(4, 3)

arr

array([[-0.33961936,  0.81082997, -0.30225737],
       [ 0.69322437, -0.97566567, -1.13947493],
       [ 1.84353878,  2.12001557,  0.32975395],
       [ 0.70970837, -1.49602363, -1.13004305]])

# 각 칼럼의 평균
arr.mean(0)

array([ 0.72671304,  0.11478906, -0.56050535])

# 각 칼럼의 표준편차
arr.std(0)

array([0.77229774, 1.43954987, 0.61620463])

standard = (arr - arr.mean(0)) / arr.std(0)

standard

array([[-1.38072708,  0.48351288,  0.41909452],
       [-0.04336238, -0.75749701, -0.93957356],
       [ 1.44610775,  1.39295383,  1.44474619],
       [-0.02201829, -1.1189697 , -0.92426715]])

브로드캐스팅 규칙 만일 이어지는 각 차원(시작부터 끝까지)에 대해 뒤에서부터 축의 크기가 일치하거나 둘 중 하나의 크기가 1이라면 두 배열은 브로드캐스팅 호환이다. 브로드캐스팅은 누락된 혹은 길이가 1인 차원에 대해 수행된다.

이전 예제에서 arr.mean(0)은 길이가 3이고 arr의 이어지는 크기 역시 3이므로 0번 축에 대해 브로드캐스팅이 가능하다. 브로드캐스팅 규칙에 따르면 1번 축에 대해 뺄셈을 하려면(각 로우에서 로우 평균값을 빼려면) 작은 크기의 배열은 (4, 1)의 크기를 가져야 한다.

arr

array([[-0.33961936,  0.81082997, -0.30225737],
       [ 0.69322437, -0.97566567, -1.13947493],
       [ 1.84353878,  2.12001557,  0.32975395],
       [ 0.70970837, -1.49602363, -1.13004305]])

row_means = arr.mean(1)

row_means.shape

(4,)

demeaned = arr - row_means # row_means.shape가 (4, 1)이 아닌 (4,)이므로 오류

print('arr.shape:', arr.shape)
print('row_means.shape:', row_means.shape)

arr.shape: (4, 3)
row_means.shape: (4,)

각 배열의 뒤에서부터 차원의 크기를 보자. 규칙에 따르면 축의 크기가 일치하거나 둘 중 하나가 1이어야 하는데 3과 None은 두 가지 규칙을 모두 만족하지 않는다(row_means.shape의 마지막 차원의 크기를 편의상 None으로 표현했다). 따라서 차원이 (4, 3)인 arr과 브로드캐스팅을 하기 위해서는 규칙에 따라 (3,)이거나 (4, 1)이어야 한다.

demeaned = arr - row_means.reshape((4, 1)) # row_means.shape를 (4,)에서 (4, 1)로 변경 후 연산

demeaned

array([[-0.39593711,  0.75451222, -0.35857511],
       [ 1.16719645, -0.50169359, -0.66550285],
       [ 0.41243602,  0.68891281, -1.10134882],
       [ 1.34849447, -0.85723753, -0.49125695]])

다른 축에 대해 브로드캐스팅하기

3차원의 경우 세 가지 차원 중 어느 하나에 대한 브로드캐스팅은 데이터를 호환되는 모양으로 재형성하면 된다.

따라서 아주 일반적인 문제는 브로드캐스팅 전용 목적으로 길이가 1인 새로운 축을 추가하는 것이다. 이에 NumPy 배열은 색인을 통해 새로운 축을 추가하는 특수한 문법을 제공한다. np.newaxis라는 이 특수한 속성을 배열의 전체 슬라이스와 함께 사용해서 새로운 축을 추가할 수 있다.

arr = np.zeros((4, 4))

print('arr:\n', arr)
print('arr.shape:', arr.shape)

arr:
 [[0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]
 [0. 0. 0. 0.]]
arr.shape: (4, 4)

arr_3d = arr[:, np.newaxis, :]

print('arr_3d:\n', arr_3d)
print('arr_3d.shape:', arr_3d.shape)

arr_3d:
 [[[0. 0. 0. 0.]]

 [[0. 0. 0. 0.]]

 [[0. 0. 0. 0.]]

 [[0. 0. 0. 0.]]]
arr_3d.shape: (4, 1, 4)

arr_1d = np.random.normal(size=3)

print('arr_1d:', arr_1d)
print('arr_1d.shape:', arr_1d.shape)

arr_1d: [-0.39090885 -0.48221392 -0.85571608]
arr_1d.shape: (3,)

arr_2d = arr_1d[:, np.newaxis]

print('arr_1d:\n', arr_2d)
print('arr_1d.shape:', arr_2d.shape)

arr_1d:
 [[-0.39090885]
 [-0.48221392]
 [-0.85571608]]
arr_1d.shape: (3, 1)

arr_2d = arr_1d[np.newaxis, :]

print('arr_2d:\n', arr_2d)
print('arr_2d.shape:', arr_2d.shape)

arr_2d:
 [[-0.39090885 -0.48221392 -0.85571608]]
arr_2d.shape: (1, 3)

다음은 3차원 배열의 각 축에 대해 브로드캐스팅하기 위해 필요한 2차원 배열의 모습을 묘사한 것이다.

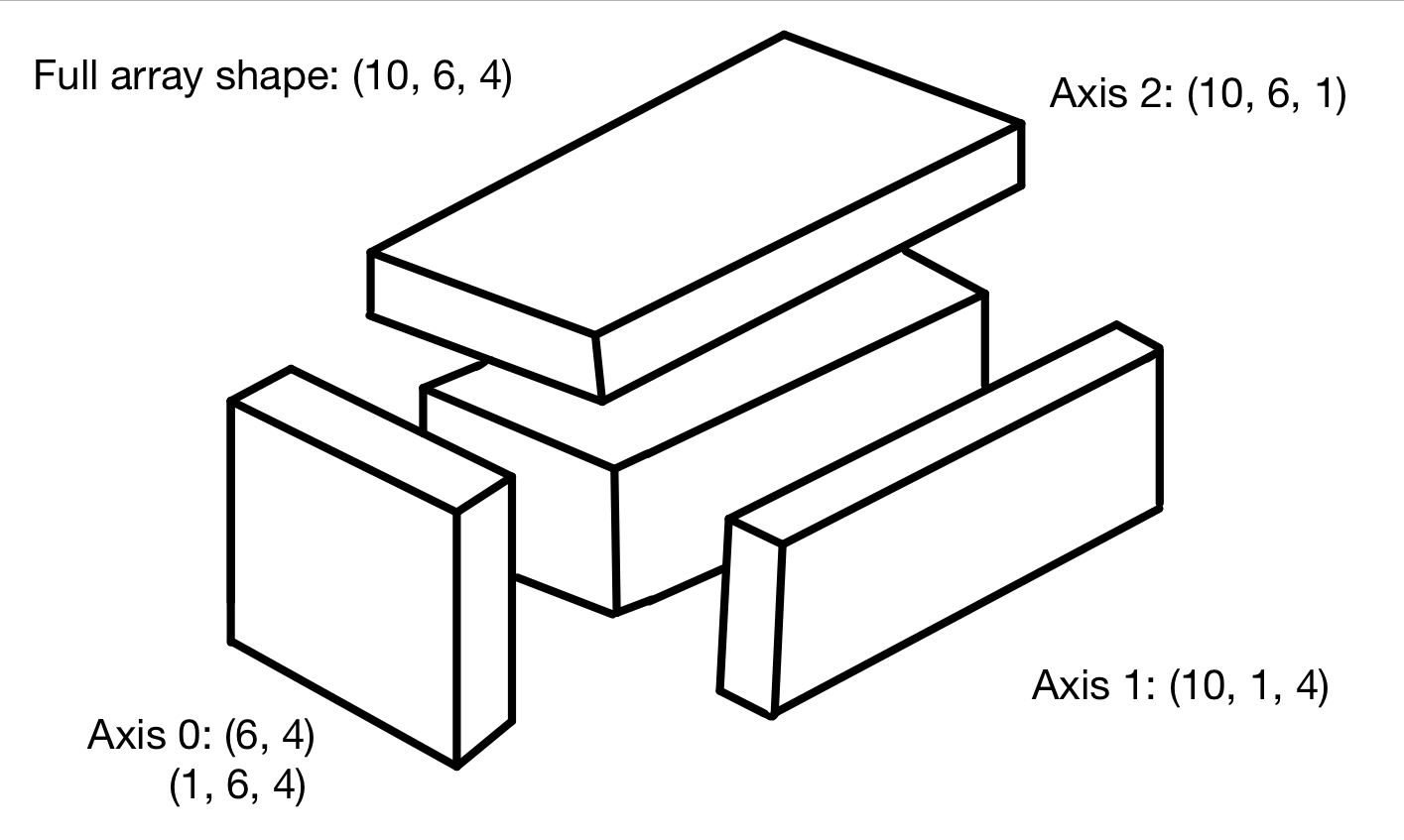
맞다. 그림이 굉장히 자유분방하다.

만약 3차원 배열에서 2번 축에 대해 평균값을 빼고 싶다면 다음과 같이 작성하면 된다.

arr = np.random.randn(10, 6, 4)

print('arr:\n', arr)
print('arr.shape:', arr.shape)

arr:
 [[[ 0.94281276 -0.48099819 -0.01565176 -0.81376381]
  [-1.15299893  0.59477599 -0.83707364 -0.07085848]
  [ 0.40154895  0.61083003 -0.27837133  0.63961449]
  [ 0.98924984  1.84374274 -0.39051702 -0.8571552 ]
  [ 0.01535811  0.89137139  0.85671358  0.22306221]
  [-1.01013147 -0.73907698  0.97788915 -0.55989274]]

 [[-0.77465836  0.81728504  2.16144999  0.18196468]
  [-0.58485983 -2.51040533  0.62857102  0.39758375]
  [ 0.89817821  0.02562351 -1.14764936 -1.48379755]
  [ 0.15406739  0.24144278  0.09560495 -0.50393066]
  [-0.71194135 -0.05359237  0.46281103 -0.27134258]
  [ 0.82933612 -0.46779385  0.58511707  0.40350212]]

 [[ 0.0592461   0.37129244 -0.93156226  0.85580148]
  [-1.49901527  0.66296026 -0.56171526  0.9890929 ]
  [ 1.23310939 -0.34477637  0.00372995 -0.08542242]
  [ 1.16270852 -0.9125005  -0.6003678  -0.5805965 ]
  [ 1.60740244  1.5486336  -0.14969084 -0.11574805]
  [ 0.23581438  0.82985336 -0.01803293  1.23484659]]

 [[ 0.62703998  0.93623899  1.06658375 -1.46856271]
  [-1.35092191 -0.53276207 -1.89839197  1.97126401]
  [ 1.19743911  0.11146755 -1.24106315 -0.54940717]
  [-0.65387014 -0.13558781 -0.91167365 -2.00649064]
  [-1.68400945  1.02265101  1.85390894  0.59314151]
  [-0.80723883 -0.73440285 -1.95386142 -1.70999654]]

 [[ 0.3706169  -0.42754691 -1.32385758  0.7304062 ]
  [-1.62505162 -0.6375124  -0.64982542  0.20136312]
  [ 0.40600162  0.58964257  0.30361022 -0.82320182]
  [-0.36757955  0.12816682  1.56079693  1.6742275 ]
  [ 0.87805016 -1.56977656 -1.92231092  1.14057029]
  [ 1.13914329  0.63337478  0.98996495  0.48883624]]

 [[ 0.51279046 -1.84950226  1.16871118 -1.01697958]
  [-0.76615118 -0.88730934 -0.16912931 -0.63086034]
  [-0.69268148  2.92657294  2.22005461  0.34456631]
  [-1.29264178  0.76165191  0.46894765  0.90944556]
  [ 0.55315473 -0.01160798  0.28100435 -0.55218003]
  [ 1.36758995 -0.69438911  1.04473693 -0.63639767]]

 [[-0.92690015  0.31499603  0.13916446  2.03316391]
  [ 0.07761613 -1.24214618  1.45043606  0.13154613]
  [ 0.11568263 -0.58099295  0.23622496 -1.34750638]
  [-1.05557763  1.39801032  0.3850367  -1.28150215]
  [ 1.72976429  1.17495105 -0.33092844  0.41189362]
  [ 0.80643511  2.00458207  0.52352635 -1.31791384]]

 [[-1.00135045 -0.06829117  0.32853681 -0.36790487]
  [-0.27567584 -0.5255316  -1.16364529 -1.84050005]
  [ 0.42818629  0.06576823 -0.20076549  0.96943035]
  [-0.87189098 -0.13625313  0.00612064  0.29550449]
  [ 0.05284839 -2.65089516 -0.56148053 -0.35684831]
  [ 0.85697709  0.91119168  0.51483418  0.35935395]]

 [[-0.60065019 -1.22720194 -0.07112048  1.70952349]
  [-0.07159157  0.67432222 -0.06791349  0.48252602]
  [ 0.14519402 -0.53926143  0.21562834  0.32033449]
  [ 0.09330904  3.20135405 -0.54283495 -2.06795195]
  [ 0.18544272  0.58673774  0.6287948  -0.13109681]
  [ 0.57313509  0.16778615 -1.38449641 -0.37653557]]

 [[ 0.67049472  0.79002667  0.45088938 -1.34972406]
  [-0.04112084  0.55616842 -0.2943434   0.06187112]
  [-0.64166176 -0.24227855  1.04015731  0.92791635]
  [ 0.11601658  0.54102234  0.03821001  0.94052071]
  [-1.07509505  1.64141032  0.21365619  0.03675847]
  [ 0.31840508 -0.11913303 -0.28998954 -0.2346899 ]]]
arr.shape: (10, 6, 4)

depth_means = arr.mean(2)

print('depth_means:\n', depth_means)
print('depth_means.shape:', depth_means.shape)

depth_means:
 [[-0.09190025 -0.36653876  0.34340554  0.39633009  0.49662632 -0.33280301]
 [ 0.59651034 -0.5172776  -0.4269113  -0.00320388 -0.14351632  0.33754036]
 [ 0.08869444 -0.10216934  0.20166014 -0.23268907  0.72264929  0.57062035]
 [ 0.290325   -0.45270298 -0.12039091 -0.92690556  0.446423   -1.30137491]
 [-0.16259535 -0.67775658  0.11901315  0.74890293 -0.36836675  0.81282981]
 [-0.29624505 -0.61336254  1.1996281   0.21185084  0.06759277  0.27038503]
 [ 0.39010606  0.10436304 -0.39414793 -0.13850819  0.74642013  0.50415742]
 [-0.27725242 -0.95133819  0.31565485 -0.17662975 -0.8790939   0.66058923]
 [-0.04736228  0.25433579  0.03547386  0.17096905  0.31746961 -0.25502768]
 [ 0.14042168  0.07064382  0.27103334  0.40894241  0.20418248 -0.08135185]]
depth_means.shape: (10, 6)

브로드캐스팅 규칙에 따르자면 ‘브로드캐스트 차원’은 작은 배열에서는 반드시 1이어야 한다. 따라서 2번 축에 대한 평균은 (10, 6)이 아니라 (10, 6, 1)로 재형성해야 한다.

demeaned = arr - depth_means[:, :, np.newaxis]

demeaned.mean(2)

array([[ 0.00000000e+00, -1.38777878e-17,  1.38777878e-17,
        -5.55111512e-17, -1.38777878e-17, -5.55111512e-17],
       [ 1.11022302e-16, -5.55111512e-17,  5.55111512e-17,
         0.00000000e+00,  0.00000000e+00,  0.00000000e+00],
       [ 2.77555756e-17,  0.00000000e+00,  0.00000000e+00,
        -2.77555756e-17,  8.32667268e-17,  2.77555756e-17],
       [ 0.00000000e+00,  0.00000000e+00,  0.00000000e+00,
         0.00000000e+00,  0.00000000e+00,  5.55111512e-17],
       [-5.55111512e-17, -2.77555756e-17, -5.55111512e-17,
         0.00000000e+00, -5.55111512e-17, -2.77555756e-17],
       [-8.32667268e-17, -4.16333634e-17, -1.66533454e-16,
         0.00000000e+00,  2.77555756e-17,  0.00000000e+00],
       [-5.55111512e-17, -2.08166817e-17,  0.00000000e+00,
         0.00000000e+00, -1.38777878e-17, -5.55111512e-17],
       [-1.38777878e-17, -5.55111512e-17,  0.00000000e+00,
        -2.77555756e-17, -8.32667268e-17, -8.32667268e-17],
       [-5.55111512e-17,  4.16333634e-17,  1.38777878e-17,
         1.11022302e-16,  4.16333634e-17, -1.38777878e-17],
       [-5.55111512e-17,  1.56125113e-17, -8.32667268e-17,
        -2.77555756e-17,  3.46944695e-17, -6.93889390e-18]])

브로드캐스팅을 이용해서 배열에 값 대입하기

배열의 인덱싱을 통해 값을 대입할 때도 산술 연산에서의 브로드캐스팅 규칙이 적용된다.

arr = np.zeros((4, 3))

print('arr:\n', arr)
print('arr.shape:', arr.shape)

arr:
 [[0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]
 [0. 0. 0.]]
arr.shape: (4, 3)

arr[:] = 5

print('arr:\n', arr)
print('arr.shape:', arr.shape)

arr:
 [[5. 5. 5.]
 [5. 5. 5.]
 [5. 5. 5.]
 [5. 5. 5.]]
arr.shape: (4, 3)

만약 값이 담긴 1차원 배열이 있고 그 배열의 칼럼에 값을 대입하고 싶다면 배열의 모양을 호환시키면 된다.

col = np.array([10, 20, 30, 40])

arr[:] = col[:, np.newaxis] # arr[:].shape: (4, 3), col[:, np.newaxis].shape: (4, 1)

arr

array([[10., 10., 10.],
       [20., 20., 20.],
       [30., 30., 30.],
       [40., 40., 40.]])

arr[:2] = [[-50], [-100]] # arr[:2].shape: (2, 3), [[-50], [-100]].shape: (2, 1)

arr

array([[ -50.,  -50.,  -50.],
       [-100., -100., -100.],
       [  30.,   30.,   30.],
       [  40.,   40.,   40.]])

고급 ufunc 사용법

많은 NumPy 사용자는 유니버셜 함수로 제공되는 빠른 원소별 연산만을 주로 사용하는데, 반복문을 작성하지 않고 좀 더 간결한 코드를 작성할 수 있는 다양한 부가적인 기능이 있다.

ufunc 인스턴스 메서드

NumPy의 이항 ufunc는 그런 특수한 벡터 연산을 수행하기 위한 특수한 메서드를 제공한다.

reduce는 하나의 배열을 받아서 순차적인 이항 연산을 통해 축에 따라 그 값을 집계해준다. 예를 들어 배열의 모든 원소를 더하는 방법으로 np.add.reduce를 사용할 수 있다.

arr = np.arange(10)

np.add.reduce(arr)

45

arr.sum()

45

시작값(add에서는 0)은 ufunc에 의존적이다. 만약 axis 인자가 넘어오면 reduce는 그 축을 따라 수행된다.

arr = np.arange(10).reshape(2, 5)

arr

array([[0, 1, 2, 3, 4],
       [5, 6, 7, 8, 9]])

np.add.reduce(arr, axis=0)

array([ 5,  7,  9, 11, 13])

np.add.reduce(arr, axis=1)

array([10, 35])

np.logical_and를 사용해서 배열의 각 로우에 있는 값이 정렬된 상태인지 검사하는 것을 생각해볼 수 있다.

np.random.seed(123456) # 동일한 난수 발생을 위해 시드값 직접 지정

arr = np.random.randn(5, 5)

arr

array([[ 0.4691123 , -0.28286334, -1.5090585 , -1.13563237,  1.21211203],
       [-0.17321465,  0.11920871, -1.04423597, -0.86184896, -2.10456922],
       [-0.49492927,  1.07180381,  0.72155516, -0.70677113, -1.03957499],
       [ 0.27185989, -0.42497233,  0.56702035,  0.27623202, -1.08740069],
       [-0.67368971,  0.11364841, -1.47842655,  0.52498767,  0.40470522]])

arr[::2].sort(axis=1) # 일부 로우[0, 2, 4]를 정렬

arr

array([[-1.5090585 , -1.13563237, -0.28286334,  0.4691123 ,  1.21211203],
       [-0.17321465,  0.11920871, -1.04423597, -0.86184896, -2.10456922],
       [-1.03957499, -0.70677113, -0.49492927,  0.72155516,  1.07180381],
       [ 0.27185989, -0.42497233,  0.56702035,  0.27623202, -1.08740069],
       [-1.47842655, -0.67368971,  0.11364841,  0.40470522,  0.52498767]])

arr[:, :-1] < arr[:, 1:] # 각 행에서 다음에 오는 수가 자신보다 크면 True, 작으면 False

array([[ True,  True,  True,  True],
       [ True, False,  True, False],
       [ True,  True,  True,  True],
       [False,  True, False, False],
       [ True,  True,  True,  True]])

np.logical_and.reduce(arr[:, :-1] < arr[:, 1:], axis=1)

array([ True, False,  True, False,  True])

logical_and.reduce는 all 메서드와 동일하다.

cumsum 메서드가 sum 메서드와 관련 있는 것처럼 accumulate는 reduce 메서드와 관련 있다.

accumulate 메서드는 누계를 담고 있는 같은 크기의 배열을 생성한다.

arr = np.arange(15).reshape((3, 5))

arr

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

np.add.accumulate(arr, axis=1) # arr.cumsum(axis=1)과 동일

array([[ 0,  1,  3,  6, 10],
       [ 5, 11, 18, 26, 35],
       [10, 21, 33, 46, 60]])

outer 메서드는 두 배열 간의 벡터곱(외적)을 계산한다.

arr = np.arange(3).repeat([1, 2, 2], axis=0)

arr

array([0, 1, 1, 2, 2])

np.multiply.outer(arr, np.arange(5))

array([[0, 0, 0, 0, 0],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 2, 4, 6, 8],
       [0, 2, 4, 6, 8]])

outer 메서드 결과의 차원은 입력한 차원의 합이 된다.

x, y = np.arange(1, 13).reshape(3, 4), np.arange(1, 6)

result = np.subtract.outer(x, y)

print('result:\n', result)
print('result.shape:', result.shape)

result:
 [[[ 0 -1 -2 -3 -4]
  [ 1  0 -1 -2 -3]
  [ 2  1  0 -1 -2]
  [ 3  2  1  0 -1]]

 [[ 4  3  2  1  0]
  [ 5  4  3  2  1]
  [ 6  5  4  3  2]
  [ 7  6  5  4  3]]

 [[ 8  7  6  5  4]
  [ 9  8  7  6  5]
  [10  9  8  7  6]
  [11 10  9  8  7]]]
result.shape: (3, 4, 5)

마지막으로 reduceat메서드는 로컬 reduce를 수행하는데, 본질적으로 로컬 reduce는 배열의 groupby 연산으로 배열의 슬라이스를 모두 집계하는 것이다. reduceat메서드는 값을 어떻게 나누고 집계할지 나타내는 경계 목록을 인자로 받는다.

arr = np.arange(10)

np.add.reduceat(arr, [0, 5, 8])

array([10, 18, 17])

이 결과는 arr[0:5], arr[5:8], arr[8:]에 대한 수행 결과(여기서는 합)다. 다른 메서드와 마찬가지로 axis 인자를 넘겨줄 수 있다.

arr = np.multiply.outer(np.arange(4), np.arange(5))

arr

array([[ 0,  0,  0,  0,  0],
       [ 0,  1,  2,  3,  4],
       [ 0,  2,  4,  6,  8],
       [ 0,  3,  6,  9, 12]])

np.add.reduceat(arr, [0, 2, 4], axis=1)

array([[ 0,  0,  0],
       [ 1,  5,  4],
       [ 2, 10,  8],
       [ 3, 15, 12]])

다음은 일부 ufunc 메서드이다.

메서드	설명
reduce(x)	연산의 연속된 적용으로 값을 집계한다.
accumulate(x)	모든 부분적 집계값을 유지한 채 값을 집계한다.
reduceat(x, bins)	로컬 reduce 또는 groupby. 연속된 데이터 슬라이스를 집계된 배열로 축소한다.
outer(x, y)	x와 y의 모든 원소 조합에 대해 연산을 적용한다. 결과 배열은 x.shape + y.shape의 모양을 가진다.

파이썬으로 사용자 정의 ufunc 작성하기

ufunc와 유사한 사용자 함수를 만들 수 있는 몇 가지 기능이 있으며 여기서는 순수 파이썬 ufunc를 살펴보겠다.

numpy.frompyfunc는 입력과 출력에 대한 표준과 함께 파이썬 함수를 인자로 취한다. 예를 들어 원소별로 합을 구하는 함수는 다음과 같이 작성할 수 있다.

def add_elements(x, y):
    return x + y

add_them = np.frompyfunc(add_elements, 2, 1) # 입력 인수의 수: 2, add_elements가 반환한 객체 수: 1 을 의미

add_them(np.arange(8), np.arange(8))

array([0, 2, 4, 6, 8, 10, 12, 14], dtype=object)

frompyfunc를 이용해서 생성한 함수는 항상 파이썬 객체가 담긴 배열을 반환하는데 이는 그다지 유용하지 못하다. 다행스럽게도 numpy.vectorize을 사용하면 반환 자료형을 지정할 수 있는 이점이 있다.

add_them = np.vectorize(add_elements, otypes=[np.float64])

add_them(np.arange(8), np.arange(8))

array([ 0.,  2.,  4.,  6.,  8., 10., 12., 14.])

이 두 함수는 ufunc 스타일의 함수를 만드는 방법을 제공하지만 각 원소를 계산하기 위해 파이썬 함수를 호출하게 되므로 NumPy의 C 기반 ufunc 반복문보다 많이 느리다.

arr = np.random.randn(10000)

%timeit add_them(arr, arr)

%timeit np.add(arr, arr)

1.68 ms ± 239 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
2.34 µs ± 140 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

관련 포스트 더 보기

NumPy01: NumPy는 무엇인가?

NumPy02: ndarray, 인덱싱, 축

NumPy03: 유니버셜 함수, 배열지향 프로그래밍, 파일 입출력, 선형대수, 난수 생성

Advanced NumPy02: 구조화된 배열과 레코드 배열, 정렬, 고급 배열 입출, 성능 팁

Example of going up and down stairs: 간단한 NumPy 실습