Example of going up and down stairs
계단 오르내리기 예제
계단 오르내리기 예제는 배열 연산의 활용을 보여줄 수 있는 간단한 애플리케이션이다. 계단 중간에서 같은 확률로 한 계단 올라가거나 내려간다고 가정하자.
순수 파이썬으로 내장 random 모듈을 사용하여 계단 오르내리기를 1,000번 수행하는 코드는 다음처럼 작성할 수 있다.
import random
position = 0 # 현재 위치
walk = [position] # 위치를 담을 배열
steps = 1000 # 오르내리는 횟수
for i in range(steps):
step = 1 if random.randint(0, 1) else -1 # 반환값이 1이면 1을, 0이면 -1을 step 변수에 할당
position += step # 현재 위치에 step을 더함
walk.append(position) # 더한 현재 위치값을 walk 배열에 추가
random.randint 함수는 인자로 들어온 a, b 사이의 랜덤한 정수를 반환한다. 즉, random.randint(0, 1)이면 0과 1을 랜덤하게 반환한다. 간단하게 step ∈ {0, 1} 로 나타낼 수 있다.
다음은 처음 100회의 계단 오르내리기를 그래프로 나타낸 것이다.
import matplotlib.pyplot as plt
plt.plot(walk[:100])
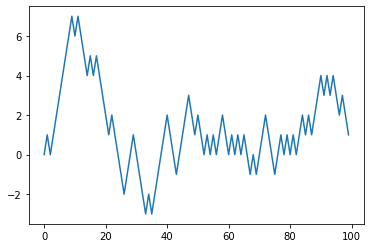
walk는 계단을 오르거나(+1) 내려간(-1) 값의 누적합이라는 사실을 알 수 있으며 배열식으로 나타낼 수 있다. 그래서 np.random 모듈을 사용해서 1,000번 수행한 결과(1, -1)를 한 번에 저장하고 누적합을 계산한다.
nsteps = 1000 # 계단을 오르내리는 횟수
draws = np.random.randint(0, 2, size=nsteps) # draws는 0 또는 1
steps = np.where(draws > 0, 1, -1) # draws가 1이면 1, 0이면 -1을 steps에 할당
walk = steps.cumsum() # 누적합 계산
walk[:5]
array([-1, 0, -1, 0, 1])
이 계단 오르내리기 예제는 계단 중간, 즉 0의 위치부터 시작해야 하므로 np.insert()로 모든 위치를 저장한 walk의 처음 값에 중간 위치인 0을 삽입했다.
walk = np.insert(walk, 0, 0)
walk[:5]
array([ 0, -1, 0, -1, 0])
draws는 0 또는 1 값을 랜덤하게 갖는다.
np.unique(draws)
array([0, 1])
마찬가지로 draws값에 따라 steps도 -1 또는 1 값을 갖는다.
np.unique(steps)
array([-1, 1])
이것으로 계단을 오르내린 위치의 최솟값과 최댓값 같은 간단한 통계를 구할 수 있다.
print('계단을 오르내린 위치의 최솟값:', walk.min())
print('계단을 오르내린 위치의 최댓값:', walk.max())
계단을 오르내린 위치의 최솟값: -22 계단을 오르내린 위치의 최댓값: 20
다음은 np.random 모듈을 이용한 계단 오르내리기를 그래프로 나타낸 것이다.
plt.plot(walk[:100])
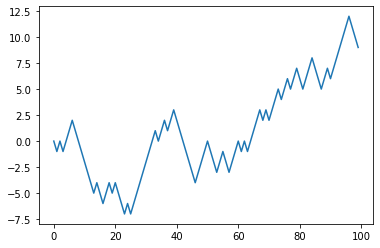
계단에서 특정 위치에 도달하기까지의 시간 같은 좀 더 복잡한 통계를 구할 수 있는데, 계단의 처음 위치에서 최초로 10칸 떨어지기까지(-10, 10) 얼마나 걸렸는지 확인해보자. np.abs(walk) >= 10으로 처음 위치에서 10칸 이상 떨어진 시점을 알려주는 불리언 배열을 얻을 수 있다.
np.abs(walk) >= 10
array([False, False, False, ..., False, False, False])
위 결과값에서는 False만 보여지지만, -10 이하 또는 10 이상인 값부터는 True이다.
np.unique(np.abs(walk) >= 10)
array([False, True])
우리는 최초의 10 혹은 -10인 시점을 구해야 하므로 불리언 배열에서 최댓값의 처음 색인을 반환하는 argmax를 사용하자(True가 최댓값이다).
(np.abs(walk) >= 10).argmax()
94
다음 방법으로도 처음 10이 되는 지점과 -10이 되는 지점을 구할 수 있다.
np.where(walk == 10)[0].min()
94
np.where(walk == -10)[0].min()
340
구한 인덱스 값을 확인해보면 10과 -10이 나온다.
walk[94]
10
walk[340]
-10
위에서 argmax를 사용했지만 argmax는 배열 전체를 모두 확인하기 때문에 효과적인 방법은 아니다. 또한 이 예제에서는 True가 최댓값임을 이미 알고 있었다.
한 번에 시뮬레이션하기
계단 오르내리기를 많은 횟수(대략 5,000회 정도) 시뮬레이션하더라도 위 코드를 조금만 수정해서 해결할 수 있다. numpy.random 함수에 크기가 2인 튜플을 넘기면 2차원 배열이 생성되고 각 칼럼에서 누적합을 구해서 5,000회의 시뮬레이션을 한 방에 처리할 수 있다.
nwalks = 5000 # 5000번의 시뮬레이션
nsteps = 1000 # 1번의 시뮬레이션마다 계단을 오르내리는 횟수
draws = np.random.randint(0, 2, size=(nwalks, nsteps)) # shape: (5000, 1000), 값: 0 또는 1
steps = np.where(draws > 0, 1, -1)
walks = steps.cumsum(1) # 각 시뮬레이션의 누적합
walks
array([[ -1, -2, -1, ..., -10, -9, -8],
[ -1, 0, -1, ..., -8, -9, -10],
[ 1, 0, 1, ..., 18, 19, 20],
...,
[ 1, 0, -1, ..., 18, 19, 18],
[ 1, 2, 1, ..., 2, 3, 2],
[ -1, -2, -3, ..., 22, 21, 20]])
마찬가지로 계단의 중간인 0을 시작점으로 하기 위해서 각 시뮬레이션의 첫번째 값에 0을 삽입해주었다. 대신 이러면 시뮬레이션의 횟수가 1,001로 증가하고 walks의 shape는 (5000, 1001)이 된다.
walks = np.insert(walks, 0, 0, axis=1) # axis가 1이라 칼럼 방향
walks
array([[ 0, -1, -2, ..., -10, -9, -8],
[ 0, -1, 0, ..., -8, -9, -10],
[ 0, 1, 0, ..., 18, 19, 20],
...,
[ 0, 1, 0, ..., 18, 19, 18],
[ 0, 1, 2, ..., 2, 3, 2],
[ 0, -1, -2, ..., 22, 21, 20]])
이제 모든 시뮬레이션에 대해 최댓값과 최솟값을 구해보자.
print('계단을 오르내린 위치의 최솟값:', walks.min())
print('계단을 오르내린 위치의 최댓값:', walks.max())
계단을 오르내린 위치의 최솟값: -149 계단을 오르내린 위치의 최댓값: 128
이 데이터에서 누적합이 30 혹은 -30이 되는 최소 시점을 계산해보자. 5,000회의 시뮬레이션 중 모든 경우가 30에 도달하지 않기 때문에 약간 까다로운데, any 메서드를 이용해서 해결할 수 있다.
hits30 = (np.abs(walks) >= 30).any(axis=1) # 시뮬레이션 별로 확인 shape: (5000,)
hits30
array([False, False, True, ..., False, False, False])
hits30.sum() # 5000회 중 3426번 30에 도달
3426
이 불리언 배열을 사용해서 walks에서 칼럼을 선택하고 절댓값이 30을 넘는 경우에 대해 축 1의 argmax 값을 구하면 처음 위치에서 30칸 이상 멀어지는 최소 횟수를 구할 수 있다.
crossing_times = (np.abs(walks[hits30]) >= 30).argmax(1)
crossing_times
array([418, 112, 768, ..., 272, 538, 906], dtype=int64)
위에서 구한 값에 대해 시뮬레이션에서 평균적으로 500회를 진행하면 절댓값이 30을 넘길 수 있다는 걸 알 수 있다.
crossing_times.mean() # 평균
500.1552831290134
다만, 표준 편차가 커서 불균형한 것 같다.
crossing_times.std() # 표준 편차
240.01280698302622
다음은 10회의 시뮬레이션 결과를 나타낸 것이다.
for i in range(10): # 10회 반복
plt.subplot(2, 5, i+1)
plt.plot(walks[i])
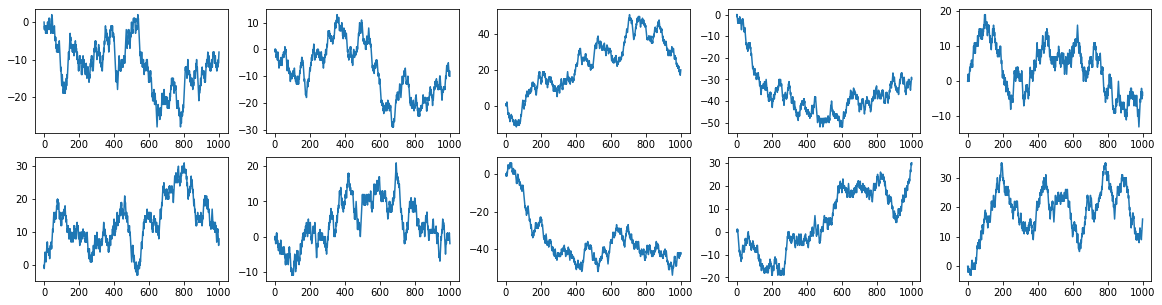
댓글남기기