유니버셜 함수, 배열지향 프로그래밍, 파일 입출력, 선형대수, 난수 생성
유니버셜 함수: 배열의 각 원소를 빠르게 처리하는 함수
ufunc라고 불리기도 하는 유니버설 함수는 ndarray 안에 있는 데이터 원소별로 연산을 수행하는 함수다. 유니버설 함수는 하나 이상의 스칼라값을 받아서 하나 이상의 스칼라 결괏값을 반환하는 간단한 함수를 고속으로 수행할 수 있는 벡터화된 래퍼 함수라고 생각하면 된다.
하나의 원소에 대응하여 값을 반환하는 유니버셜 함수를 단항 유니버셜 함수라고 한다. 또한, 2개의 인자를 취해서 단일 배열을 반환하는 함수는 이항 유니버셜 함수라고 한다.
여러 개의 배열을 반환하는 유니버셜 함수도 있다. 예를 들어 modf는 분수를 받아서 몫과 나머지를 함께 반환한다.
유니버셜 함수는 선택적으로 out 인자를 취해 계산 결과를 따로 저장할 수도 있다.
다음은 사용가능한 단항 유니버셜 함수다.
| 함수 | 설명 |
|---|---|
| abs, fabs | 각 원소(정수, 부동소수점수, 복소수)의 절댓값을 구한다. 복소수가 아닌 경우에는 빠른 연산을 위해서 fabs를 사용한다. |
| sqrt | 각 원소의 제곱근을 계산한다. arr**0.5와 동일하다. |
| square | 각 원소의 제곱을 계산한다. arr**2와 동일하다. |
| exp | 각 원소에서 지수 ex을 계산한다. |
| log, log10, log2, log1p | 각각 자연로그, 로그 10, 로그 2, 로그 (1+x) |
| sign | 각 원소의 부호를 계산한다. 1(양수), 0(영), -1(음수) |
| ceil | 각 원소의 소수자리를 올린다. 각 원소의 값보다 같거나 큰 정수 중 가장 작은 정수를 반환한다. |
| floor | 각 원소의 소수자리를 내린다. 각 원소의 값보다 작거나 같은 정수 중 가장 작은 수를 반환한다. |
| rint | 각 원소의 소수자리를 반올림한다. dtype은 유지된다. |
| modf | 각 원소의 몫과 나머지를 각각의 배열로 반환한다. |
| isnan | 각 원소가 숫자가 아닌지(Not a Number; NaN)를 나타내는 불리언 배열을 반환한다. |
| isfinite, isinf | 각각 배열의 각 원소가 유한한지(non-inf, non-NaN) 무한한지 나타내는 불리언 배열을 반환한다. |
| cos, cosh, sin, sinh, tan, tanh | 일반 삼각함수와 쌍곡삼각함수 |
| arccos, arccosh, arcsin, arcsinh, arctan, arctanh | 역삼각함수 |
| logical_not | 각 원소의 논리 부정(not) 값을 계산한다. ~arr과 동일하다. |
다음은 사용가능한 이항 유니버셜 함수다.
| 함수 | 설명 |
|---|---|
| add | 두 배열에서 같은 위치의 원소끼리 더한다. |
| subtract | 첫 번째 배열의 원소에서 두 번째 배열의 원소를 뺀다. |
| multiply | 배열의 원소끼리 곱한다. |
| divide, floor_divide | 첫 번째 배열의 원소를 두 번째 배열의 원소로 나눈다. floor_divide는 몫만 취한다. |
| power | 첫 번째 배열의 원소를 두 번째 배열의 원소만큼 제곱한다. |
| maximum, fmax | 각 배열의 두 원소 중 큰 값을 반환한다. fmax는 NaN을 무시한다. |
| minimum, fmin | 각 배열의 두 원소 중 작은 값을 반환한다. fmin은 NaN을 무시한다. |
| mod | 첫 번째 배열의 원소를 두 번째 배열의 원소로 나눈 나머지를 구한다. |
| copysign | 첫 번째 배열의 원소의 기호를 두 번째 배열의 원소의 기호로 바꾼다. 0은 양수 취급한다. |
| greater, greater_equal, less, less_equal, equal, not_equal | 각각 두 원소 간의 >, >=, <, <=, ==, != 비교 연산 결과를 불리언 배열로 반환한다. |
| logical_and, logical_or, logical_xor | 각각 두 원소 간의 &, |, ^논리 연산 결과를 반환한다. |
배열을 이용한 배열지향 프로그래밍
NumPy 배열을 사용하면 반복문을 작성하지 않고 간결한 배열 연산을 사용해 많은 종류의 데이터 처리 작업을 할 수 있다. 배열 연산을 사용해서 반복문을 명시적으로 제거하는 기법을 흔히 벡터화라고 부르는데, 일반적으로 벡터화된 배열에 대한 산술 연산은 순수 파이썬 연산에 비해 2~3배에서 많게는 수십, 수백 배까지 빠르다.
간단한 예로 값이 놓여 있는 그리드에서 $\sqrt{x^2 + y^2}$을 계산한다고 하자. np.meshgrid 함수는 두 개의 1차원 배열을 받아서 가능한 모든 (x, y) 짝을 만들 수 있는 2차원 배열 두 개를 반환한다.
import numpy as np
잠깐 np.meshgrid에 대해 간단히 알아보자!
points = np.arange(1, 6, 1) # 1부터 5까지 1씩 증가하는 값들의 배열
print(points)
[1 2 3 4 5]
xs, ys = np.meshgrid(points, points)
print('xs:\n',xs) # x축 방향으로 points 나열
print('ys:\n',ys) # y축 방향으로 points 나열
xs: [[1 2 3 4 5] [1 2 3 4 5] [1 2 3 4 5] [1 2 3 4 5] [1 2 3 4 5]] ys: [[1 1 1 1 1] [2 2 2 2 2] [3 3 3 3 3] [4 4 4 4 4] [5 5 5 5 5]]
plt.scatter(xs, ys) # 각 위치에 맞게 점을 찍어 봄(1, 1), (2, 1), (3, 1), ..., (4, 5), (5, 5)
plt.show()
np.meshgrid는 지정한 배열에 맞는 격자를 만들어 준다. 다시 원문으로 돌아와 $\sqrt{x^2 + y^2}$을 계산해 보겠다.
points = np.arange(-5, 5, 0.01) # -5부터 4.99까지 0.01씩 증가하는 값들의 배열
xs, ys = np.meshgrid(points, points)
print('xs:\n', xs)
print('ys:\n', ys)
xs: [[-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99] ... [-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99] [-5. -4.99 -4.98 ... 4.97 4.98 4.99]] ys: [[-5. -5. -5. ... -5. -5. -5. ] [-4.99 -4.99 -4.99 ... -4.99 -4.99 -4.99] [-4.98 -4.98 -4.98 ... -4.98 -4.98 -4.98] ... [ 4.97 4.97 4.97 ... 4.97 4.97 4.97] [ 4.98 4.98 4.98 ... 4.98 4.98 4.98] [ 4.99 4.99 4.99 ... 4.99 4.99 4.99]]
이제 그리드 상의 두 포인트로 간단하게 계산을 적용할 수 있다.
z = np.sqrt(xs ** 2 + ys ** 2) # sqrt(x^2 + y^2)
z
array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
7.06400028],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
...,
[7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
7.04279774],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568]])
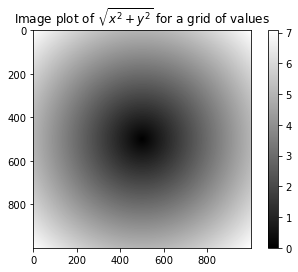
시각화를 해주는 matplotlib(맷플롯립)을 이용해서 이 2차원 배열을 시각화할 수 있다.
import matplotlib.pyplot as plt
plt.imshow(z, cmap=plt.cm.gray); plt.colorbar()
plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
plt.show()
배열 연산으로 조건절 표현하기
numpy.where 함수는 x if 조건 else y 같은 삼항식의 벡터화된 버전이다. 다음과 같은 불리언 배열 하나와 값이 들어 있는 두 개의 배열이 있다고 하자.
xarr = np.array([1, 2, 3, 4, 5]) # 값이 들어 있는 배열
yarr = np.array([-1, -2, -3, -4, -5]) # 값이 들어 있는 배열
cond = np.array([True, False, True, True, False]) # 불리언 배열
cond의 값이 True일 때는 xarr의 값을 취하고 아니면 yarr의 값을 취하고 싶다면 리스트 표기법list comprehension을 이용해서 다음처럼 작성할 수 있다.
result = [(x if c else y)
for x, y, c in zip(xarr, yarr, cond)]
for c, v in zip(cond, result):
print('{0}: {1}'.format(c, v)) # cond가 True일 때는 xarr, False일 때는 yarr
True: 1 False: -2 True: 3 True: 4 False: -5
이 방법은 순수 파이썬으로 수행되기 때문에 큰 배열을 빠르게 처리하지 못하고 다차원 배열에서는 사용할 수 없는 문제가 있다. 이를 대신해 np.where을 사용하면 아주 간결하게 사용할 수 있다.
result = np.where(cond, xarr, yarr)
for c, v in zip(cond, result):
print('{0}: {1}'.format(c, v)) # cond가 True일 때는 xarr, False일 때는 yarr
True: 1 False: -2 True: 3 True: 4 False: -5
np.where의 두 번째와 세 번째 인자는 배열이 아니어도 상관없다. 둘 중 하나 혹은 둘 다 스칼라값이어도 동작한다. 데이터 분석에서 일반적인 where의 사용은 다른 배열에 기반한 새로운 배열을 생성한다. 임의로 생성된 데이터가 들어 있는 행렬이 있고 양수는 모두 2로, 음수는 모두 -2로 바꾸려면 np.where를 사용해서 쉽게 처리할 수 있다.
arr = np.random.randn(4, 4)
arr
array([[-0.02976962, -0.01458426, 1.42759411, -0.88031711],
[-1.19553913, -0.74505178, -0.3956748 , 0.06363249],
[ 0.71457475, 1.70660529, -0.15164689, 1.06711576],
[-0.49864073, -0.17354365, -1.07199579, -0.17578479]])
arr > 0 # 0보다 큰 값에 대해서는 True, 작으면 False
array([[False, False, True, False],
[False, False, False, True],
[ True, True, False, True],
[False, False, False, False]])
np.where(arr > 0, 2, -2) # arr > 0의 조건절에 대해 True면 2, False면 -2를 대입 배열
array([[-2, -2, 2, -2],
[-2, -2, -2, 2],
[ 2, 2, -2, 2],
[-2, -2, -2, -2]])
앞서 말한 대로 np.where는 스칼라값과 배열을 조합할 수 있다. 예를 들어 arr의 모든 양수를 2로 바꿀 수 있다.
np.where(arr > 0, 2, arr) # 양수인 경우에만 2를 대입한다.
array([[-0.02976962, -0.01458426, 2. , -0.88031711],
[-1.19553913, -0.74505178, -0.3956748 , 2. ],
[ 2. , 2. , -0.15164689, 2. ],
[-0.49864073, -0.17354365, -1.07199579, -0.17578479]])
np.where로 넘기는 배열은 그냥 크기만 같은 배열이거나 스칼라값이 될 수 있다.
수학 메서드와 통계 메서드
배열 전체 혹은 배열에서 한 축을 따르는 자료에 대한 통계를 계산하는 수학 함수는 배열 메서드로 사용할 수 있다. 전체의 합(sum)이나 평균(mean), 표준편차(std)는 NumPy의 최상위 함수를 이요하거나 배열의 인스턴스 메서드를 사용해서 구할 수 있다.
arr = np.random.randn(5, 4)
arr
array([[-0.40803355, -1.44763423, -0.46975607, 1.13041391],
[ 0.55472786, 2.51064512, 0.91108982, 0.34050927],
[ 1.11245197, 2.13788859, 0.11894154, -1.43108026],
[-0.80010396, 0.57906191, 0.07198797, 0.21484875],
[ 0.22236126, -0.02624284, -1.46658882, 1.31371429]])
arr.mean() # 배열의 인스턴스 메서드
0.25846012682626107
np.mean(arr) # NumPy의 최상위 함수
0.25846012682626107
mean이나 sum 같은 함수는 선택적으로 axis 인자를 받아서 해당 axis에 대한 통계를 계산하고 한 차수 낮은 배열을 반환한다.
arr.mean(axis=1) # (5, 4) -> (5,)
array([-0.29875248, 1.07924302, 0.48455046, 0.01644867, 0.01081097])
arr.sum(axis=0) # (5, 4) -> (4,)
array([ 0.68140358, 3.75371854, -0.83432555, 1.56840597])
axis=0 은 기준을 행(로우)로 잡으라는 의미이며, axis=1은 기준을 열(칼럼)으로 잡으라는 의미이다.
cumsum과 cumprod 메서드는 중간 계산값을 담고 있는 배열을 반환한다.
arr = np.array([0, 1, 2, 3, 4, 5, 6, 7])
arr.cumsum()
array([ 0, 1, 3, 6, 10, 15, 21, 28])
다차원 배열에서 cumsum같은 누산 함수는 같은 크기의 배열을 반환한다. 하지만 축을 지정하여 부분적으로 계산하면 낮은 차수의 슬라이스를 반환한다.
arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
arr
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
arr.cumsum(axis=0)
array([[ 0, 1, 2],
[ 3, 5, 7],
[ 9, 12, 15]])
arr.cumsum(axis=1)
array([[ 0, 1, 3],
[ 3, 7, 12],
[ 6, 13, 21]])
다음은 기본 배열 통계 메서드다.
| 메서드 | 설명 |
|---|---|
| sum | 배열 전체 혹은 특정 축에 대한 모든 원소의 합을 계산한다. 크기가 0인 배열에 대한 sum 결과는 0이다. |
| mean | 산술 평균을 구한다. 크기가 0인 배열에 대한 mean 결과는 NaN이다. |
| std, var | 각각 표준편차(std)와 분산(var)을 구한다. 선택적으로 자유도를 줄 수 있으며 분모의 기본 값은 n이다. |
| min, max | 최솟값과 최댓값 |
| argmin, argmax | 최소 원소의 인덱스값과 최대 원소의 인덱스값 |
| cumsum | 각 원소의 누적합 |
| cumprod | 각 원소의 누적곱 |
불리언 배열을 위한 메서드
이전 메서드의 불리언값을 1(True) 또는 0(False)으로 강제할 수 있다. 따라서 sum메서드를 실행하면 불리언 배열에서 True인 원소의 개수를 셀 수 있다.
arr = np.random.randn(100)
(arr > 0).sum() # 양수인 원소의 개수
55
any와 all 메서드는 불리언 배열에 특히 유용하다. any 메서드는 하나 이상의 값이 True인지 검사하고, all 메서드는 모든 원소가 True인지 검사한다.
bools = np.array([False, False, True, False])
bools.any() # True 값이 1개 있으므로 True 반환
True
bools.all() # 모두 원소가 True가 아니므로 False 반환
False
이들 메서드는 불리언 배열이 아니어도 동작하는데, 0이 아닌 원소는 모두 True로 간주한다.
arr
array([-0.90724395, -0.62877129, 0.20718284, -0.30639522, 0.30563246,
0.64600853, 0.36622221, -0.20823254, 0.56306029, 0.08465395,
0.17931446, -1.31047274, 1.31780143, 1.19431253, 0.77679295,
0.66257028, 0.81578488, -0.10122762, -1.56994089, 0.7210543 ,
1.57814075, -0.77683207, 0.53661484, 1.55243271, -0.70011526,
-0.92437677, 0.06512332, -1.28821736, -0.42673967, 2.11522999,
-0.06873509, 0.10835011, 0.16375313, 1.13753012, 0.60778277,
-0.61662619, 0.90796244, 0.10654738, 1.53838342, -0.68642838,
1.10722921, 0.05376696, -0.22741643, 0.19152851, 0.61814316,
-0.7838633 , -2.52647135, -0.55955101, -1.62492829, 1.57278237,
-0.84292233, 0.62413717, -0.58376745, -1.10119351, -2.19279612,
2.01211672, 0.17202275, 2.33114224, -1.38486633, -0.95180022,
0.67905259, 0.27600726, 2.29801415, -0.82937238, 0.91102118,
-2.0647726 , -1.36350404, 1.16755995, 0.72074234, 2.39359361,
0.46767095, 1.00898659, 1.25154436, -0.30093986, -3.05331187,
-0.34446774, 0.42159384, -1.93885532, 1.52567005, -0.83601494,
0.12425241, -2.53676551, -1.13924765, 0.91451041, -0.98690224,
-0.33942484, -2.00901952, 0.32953966, -1.33603297, 0.21150542,
-1.94545459, -0.73211461, -1.23605764, -0.48188263, 0.60539548,
0.50564888, -0.30340103, 0.8815487 , 0.05362069, 0.57654203])
arr.any()
True
arr.all() # 음수도 True로 간주하므로 True가 나왔다.
True
정렬
넘파이의 행렬 정렬은 np.sort()와 같이 넘파이에서 sort()를 호출하는 방식과 ndarray.sort()와 같이 행렬 자체에서 sort()를 호출하는 방식이 있다. 두 방식의 차이는 np.sort()의 경우 원 행렬은 그대로 유지한 채 정렬된 결과를 가지고 있는 복사본을 반환하며, ndarray.sort()는 원 행렬 자체를 정렬한 형태로 변환하며 반환 값은 None이다.
org_array = np.array([3, 1, 9, 5, 7, 2])
print('원본 행렬:', org_array)
# np.sort()로 정렬
sort_array1 = np.sort(org_array)
print('np.sort() 호출 후 반환된 정렬 행렬:', sort_array1)
print('no.sort() 호출 후 원본 행렬:', org_array)
# ndarray.sort()로 정렬
sort_array2 = org_array.sort()
print('org_array.sort() 호출 후 반환된 행렬:', sort_array2)
print('org_array.sort() 호출 후 원본 행렬:', org_array)
원본 행렬: [3 1 9 5 7 2] np.sort() 호출 후 반환된 정렬 행렬: [1 2 3 5 7 9] no.sort() 호출 후 원본 행렬: [3 1 9 5 7 2] org_array.sort() 호출 후 반환된 행렬: None org_array.sort() 호출 후 원본 행렬: [1 2 3 5 7 9]
arr.sort()
arr
array([-1.55777475, -0.92121968, -0.21422782, 0.08067499, 0.89476559,
0.9563294 ])
np.sort()나 ndarray.sort() 모두 기본적으로 오름차순으로 행렬 내 원소를 정렬한다. 내림차순으로 정렬하기 위해서는 [::-1]을 적용하여 np.sort()[::-1]과 같이 사용하면 된다.
np.sort(org_array)[::-1]
array([9, 7, 5, 3, 2, 1])
행렬이 2차원 이상일 경우에 axis 축 값 설정을 통해 로우 방향, 또는 칼럼 방향으로 정렬을 수행할 수 있다.
array2d = np.array([[8, 12],
[7, 1]])
sort_array2d_axis0 = np.sort(array2d, axis=0)
print('로우 방향으로 정렬:\n', sort_array2d_axis0)
sort_array2d_axis1 = np.sort(array2d, axis=1)
print('칼럼 방향으로 정렬:\n', sort_array2d_axis1)
로우 방향으로 정렬: [[ 7 1] [ 8 12]] 칼럼 방향으로 정렬: [[ 8 12] [ 1 7]]
집합 관련 함수
NumPy는 1차원 ndarray를 위한 몇 가지 기본적인 집합 연산을 제공한다. np.unique 는 배열 내에서 중복된 원소를 제거하고 남은 원소를 정렬된 형태로 반환하는 함수다.
names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
np.unique(names)
array(['Bob', 'Joe', 'Will'], dtype='< U4')
ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])
np.unique(ints)
array([1, 2, 3, 4])
np.in1d 함수는 두 개의 배열을 인자로 받아서 첫 번째 배열의 원소가 두 번째 배열의 원소를 포함하는지 타나내는 불리언 배열을 반환한다.
values = np.array([6, 0, 0, 3, 2, 5, 6])
np.in1d(values, [2, 3, 6])
array([ True, False, False, True, True, False, True])
다음은 NumPy에서 제공하는 배열 집합 함수이다.
| 메서드 | 설명 |
|---|---|
| unique(x) | 배열 x에서 중복된 원소를 제거한 뒤 정렬하여 반환한다. |
| intersect1d(x, y) | 배열 x와 y에 공통적으로 존재하는 원소를 정렬하여 반환한다. |
| union1d(x, y) | 두 배열의 합집합을 반환한다. |
| in1d(x, y) | x의 원소가 y의 원소에 포함되는지 나타내는 불리언 배열을 반환한다. |
| setdiff1d(x, y) | x와 y의 차집합을 반환한다. |
| setxor1d(x, y) | 한 배열에는 포함되지만 두 배열 모두에는 포함되지 않는 원소들의 집합인 대칭차집합을 반환한다. |
x = np.array([1, 3, 5, 7, 9])
y = np.array([9, 8, 7, 6, 5, 4, 3])
np.intersect1d(x, y) # 공통적으로 존재하는 원소를 정렬하여 반환
array([3, 5, 7, 9])
배열 데이터의 파일 입출력
NumPy는 디스크에서 텍스트나 바이너리 형식의 데이터를 불러오거나 저장할 수 있다.
np.save와 np.load는 배열 데이터를 효과적으로 디스크에 저장하고 불러오기 위한 함수다. 배열은 기본적으로 압축되지 않은 원시(가공되지 않은) 바이너리 형식의 .npy 파일로 저장된다.
arr = np.arange(10)
np.save('some_array', arr)
저장되는 파일 경로가 .npy로 끝나지 않으면 자동적으로 확장자가 추가된다. 이렇게 저장된 배열은 np.load를 이용해서 불러올 수 있다.

np.load('some_array.npy')
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
np.savez함수를 이용하면 여러 개의 배열을 압축된 형식으로 저장할 수 있는데, 저장하려는 배열을 키워드 인자 형태로 전달한다.
np.savez('array_archive.npz', a=arr, b=arr)

npz 파일을 불러올 때는 각각의 배열을 필요할 때 불러올 수 있도록 사전 형식의 객체에 저장한다.
arch = np.load('array_archive.npz')
arch['b']
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
압축이 잘되는 형식의 데이터라면 대신 numpy.savez_compressed를 사용하자.
np.savez_compressed('arrays_compressed.npz', a=arr, b=arr)

선형대수
행렬의 곱셈, 분할, 행렬식 그리고 정사각 행렬 수학 같은 선형대수는 배열을 다루는 라이브러리에서 중요한 부분이다. 행렬 내적은 행렬 곱이며, 두 행렬 A와 B의 내적은 np.dot()을 이용해 계산이 가능하다. 행렬 내적의 특성으로 왼쪽 행렬의 열 개수와 오른쪽 행렬의 행 개수가 동일해야 내적 연산이 가능하다.
A = np.array([[1, 2, 3], # A의 크기는 (2, 3)
[4, 5, 6]])
B = np.array([[7, 8], # B의 크기는 (3, 2)
[9, 10],
[11, 12]])
dot_product = np.dot(A, B)
print('행렬 내적의 결과:\n', dot_product)
행렬 내적의 결과: [[ 58 64] [139 154]]
np.dot(x, y)는 x.dot(y)와 동일하다.
A.dot(B)
array([[ 58, 64],
[139, 154]])
2차원 배열과 곱셈이 가능한 크기의 1차원 배열 간의 행렬 곱셈의 결과는 1차원 배열이다.
np.dot(A, np.ones(3)) # 6 = 1 + 2 + 3, 15 = 4 + 5 + 6
array([ 6., 15.])
파이썬 3.5부터 사용할 수 있는 @기호는 행렬 곱셈을 수행하는 연산자다.
A @ np.ones(3)
array([ 6., 15.])
원 행렬에서 행과 열 위치를 교환한 원소로 구성한 행렬을 그 행렬의 전치 행렬이라고 한다. 이때 행렬 A의 전치 행렬은 AT와 같이 표기한다.
A = np.array([[1, 2],
[3, 4]])
transpose_mat = np.transpose(A)
print('A의 전치 행렬:\n', transpose_mat)
A의 전치 행렬: [[1 3] [2 4]]
numpy.linalg는 행렬의 분할과 역행렬, 행렬식과 같은 것들을 포함하고 있다. 이는 MATLAB, R 같은 언어에서 사용하는 표준 포트란 라이브러리인 BLAS, LAPACK 또는 Intel MKLMath Kernel Library(NumPy 빌드에 따라 다르다)을 사용해서 구현되었다. 다음은 자주 사용하는 선형대수 함수이다.
| 함수 | 설명 |
|---|---|
| diag | 정사각 행렬의 대각/비대각 원소를 1차원 배열로 반환하거나, 1차원 배열을 대각선 원소로 하고 나머지는 0으로 채운 단위행렬을 반환한다. |
| dot | 행렬 곱셈(내적) |
| trace | 행렬의 대각선 원소의 합을 계산한다. |
| det | 행렬식을 계산한다. |
| eig | 정사각 행렬의 고윳값과 고유벡터를 계산한다. |
| inv | 정사각 행렬의 역행렬을 계산한다. |
| pinv | 정사각 행렬의 무어-펜로즈 유사역원 역행렬을 구한다. |
| qr | QR 분해를 계산한다. |
| svd | 특잇값 분해(SVD)를 계산한다. |
| solve | A가 정사각 행렬일 때 Ax = b를 만족하는 x를 구한다. |
| lstsq | Ax = b를 만족하는 최소제곱해를 구한다. |
난수 생성
numpy.random 모듈은 파이썬 내장 random함수를 보강하여 다양한 종류의 확률분포로부터 효과적으로 표본값을 생성하는 데 주로 사용된다. 예를 들어 normal을 사용하여 표준정규분포로부터 4x4 크기의 표본을 생성할 수 있다.
samples = np.random.normal(size=(4, 4))
samples
array([[-0.35707674, 1.17394871, -0.4338118 , -0.57904352],
[-0.09021765, -0.19559481, -0.88596855, 1.02610079],
[ 1.05375425, -0.62062368, 1.73299383, 0.14176114],
[-1.43600832, 0.67144311, 1.25738013, 1.24417756]])
이에 비해 파이썬 내장 random 모듈은 한 번에 하나의 값만 생성할 수 있다. 다음 성능 비교에서 알 수 있듯이 numpy.random은 매우 큰 표본을 생성하는데 파이썬 내장 모듈보다 수십 배 이상 빠르다.
from random import normalvariate
N = 1000000
%timeit samples = [normalvariate(0, 1) for _ in range(N)]
%timeit np.random.normal(size=N)
906 ms ± 29.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each) 24 ms ± 1.45 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)
이를 엄밀하게는 유사 난수라고 부르는데, 난수 생성기의 시드값에 따라 정해진 난수를 알고리즘으로 생성하기 때문이다. NumPy 난수 생성기의 시드값은 np.random.seed를 이용해서 변경할 수 있다.
np.random.seed(1234)
numpy.random에서 제공하는 데이터를 생성할 수 있는 함수들은 전역 난수 시드값을 이용한다.
numpy.random.RandomState를 이용해서 다른 난수 생성기로부터 격리된 난수 생성기를 만들 수 있다.
rng = np.random.RandomState(1234)
rng.randn(10)
array([ 0.47143516, -1.19097569, 1.43270697, -0.3126519 , -0.72058873,
0.88716294, 0.85958841, -0.6365235 , 0.01569637, -2.24268495])
다음은 numpy.random에 포함된 일부 함수다.
| 함수 | 설명 |
|---|---|
| seed | 난수 생성기의 시드를 지정한다. |
| permutation | 순서를 임의로 바꾸거나 임의의 순열을 반환한다. |
| shuffle | 리스트나 배열의 순서를 뒤섞는다. |
| rand | 균등분포에서 표본을 추출한다. |
| randint | 주어진 최소/최대 범위 안에서 임의의 난수를 추출한다. |
| randn | 표준편차가 1이고 평균값이 0인 정규분포(매트랩과 같은 방식)에서 표본을 추출한다. |
| binomial | 이항분포에서 표본을 추출한다. |
| normal | 정규분포(가우시안)에서 표본을 추출한다. |
| beta | 베타분포에서 표본을 추출한다. |
| chisquare | 카이제곱분포에서 표본을 추출한다. |
| gamma | 감마분포에서 표본을 추출한다. |
| uniform | 균등 [0, 1) 분포에서 표본을 추출한다. |
댓글남기기