통계 분석 기법과 머신러닝 맛보기
통계 분석 기법을 이용한 가설 검정
기술 통계와 추론 통계
통계 분석은 기술 통계와 추론 통계로 나눌 수 있다. 데이터를 요약해 설명하는 통계 분석 기법을 기술 통계descriptive statistics라고 한다. 예를 들어 사람들이 받는 월급을 집계해 전체 월급 평균을 구한다면 이는 ‘기술 통계 분석’이다.
추론 통계inferential statistics는 단순히 숫자를 요약하는 것을 넘어 어떤 값이 발생할 확률을 계산하는 통계 분석 기법이다. 예를 들어 데이터에서 성별에 따라 월급에 차이가 있는 것으로 나타났을 때, 이런 차이가 우연히 발생할 확률을 계산한다. 만약 이런 차이가 우연히 나타날 확률이 작다면 성별에 따른 월급 차이가 통계적으로 유의하다statistically significant고 결론을 내린다. 반대로 이런 차이가 우연히 나타날 확률이 크다면 성별에 따른 월급 차이가 통계적으로 유의하지 않다not statistically significant고 결론을 내린다.
일반적으로 통계 분석을 수행했다는 것은 추론 통계를 이용해 가설 검정을 했다는 의미이다. 기술 통계 분석에서 집단 간 차이가 있는 것으로 나타났더라도 이는 우연에 의한 차이일 수 있다. 데이터를 이용해 신뢰할 수 있는 결론을 내리려면 유의확률을 계산하는 통계적 가설 검정 절차를 거쳐야 한다.
통계적 가설 검정
유의확률을 이용해 가설을 검정하는 방법을 통계적 가설 검정statistical hypothesis test이라고 한다. 유의확률significance probability, p-value은 실제로는 집단 간 차이가 없는데 우연히 차이가 있는 데이터가 추출될 확률을 의미한다.
통계 분석을 한 결과 유의확률이 크게 나타났다면 ‘집단 간 차이가 통계적으로 유의하지 않다’고 해석한다. 이는 실제로 차이가 없더라도 우연에 의해 이런 정도의 차이가 관찰될 가능성이 크다는 의미다. 반대로 유의확률이 작다면 ‘집단 간 차이가 통계적으로 유의하다’고 해석한다. 이는 실제로 차이가 없는데 우연히 이런 정도의 차이가 관찰될 가능성이 작다, 즉 우연이라고 보기 힘들다는 의미다.
이 장에서는 통계적 가설 검정 기법 중에서 두 집단의 평균에 차이가 있는지 검정하는 t 검정과 두 변수가 관련이 있는지 검정하는 상관분석을 알아보겠다.
t 검정 - 두 집단의 평균 비교하기
t 검정t-test은 두 집단의 평균에 통계적으로 유의한 차이가 있는지 알아볼 때 사용하는 통계 분석 기법이다. t 검정을 하는 방법을 알아보자.
compact 자동차와 suv 자동차의 도시 연비 t 검정
mpg 데이터를 이용해 ‘compact’ 자동차와 ‘suv’ 자동차의 도시 연비 차이가 통계적으로 유의한지 알아보자.
먼저 mpg 데이터를 불러와 category가 ‘compact’인 자동차와 ‘suv’인 자동차의 빈도와 cty 평균을 구해보자. 출력 결과를 보면 도시 연비 평균이 ‘compact’는 20, ‘suv’는 13이므로 ‘suv’보다 ‘compact’가 더 높다.
import pandas as pd
mpg = pd.read_csv('mpg.csv')
# 기술 통계 분석
mpg.query('category in ["compact", "suv"]') \
.groupby('category', as_index=False) \
.agg(n=('category', 'count'),
mean=('cty', 'mean'))
| category | n | mean | |
|---|---|---|---|
| 0 | compact | 47 | 20.12766 |
| 1 | suv | 62 | 13.50000 |
앞에서 구한 평균 차이가 통계적으로 유의한지 t 검정을 수행해 알아보자. 먼저 mpg에서 category가 ‘compact’인 행과 ‘suv’인 행의 cty를 추출해 각각 변수에 할당하자.
compact = mpg.query('category == "compact"')['cty']
suv = mpg.query('category == "suv"')['cty']
scipy 패키지의 ttest_ind()를 이용하면 t 검정을 할 수 있다. 앞에서 추출한 두 변수를 ttest_ind()에 나열하면 된다.
t 검정은 비교하는 집단의 분산(값이 퍼져 있는 정도)이 같은지 여부에 따라 적용하는 공식이 다르다. 여기서는 집단 간 분산이 같다고 가정하고 equal_var = True를 입력하겠다.
# t-test
from scipy import stats
stats.ttest_ind(compact, suv, equal_var=True)
Ttest_indResult(statistic=11.917282584324107, pvalue=2.3909550904711282e-21)
출력 결과에서 ‘pvalue’가 유의확률을 의미한다. 일반적으로 유의확률 5%를 판단 기준으로 삼고, p-value가 0.05 미만이면 ‘집단 간 차이가 통계적으로 유의하다’고 해석한다. 실제로는 차이가 없는데 이런 정도의 차이가 유연히 관찰될 확률이 5%보다 작다면, 이 차이를 우연이라고 보기 어렵다고 결론을 내리는 것이다.
‘pvalue=2.3909550904711282e-21’은 유의확률이 ‘2.3909550904711282 앞에 0이 21개 있는 값(2.3909550904711282 x 10의 -21승)’보다 작다는 의미이다. p-value가 0.05보다 작기 때문에 이 분석 결과는 ‘compact와 suv 간 평균 도시 연비 차이가 통계적으로 유의하다’고 결론 내릴 수 있다.
일반 휘발유와 고급 휘발유의 도시 연비 t 검정
이번에는 일반 휘발유regular를 사용하는 자동차와 고급 휘발유premium를 사용하는 자동차의 도시 연비 차이가 통계적으로 유의한지 알아보겠다. 두 연료를 사용하는 자동차의 빈도와 cty 평균을 구한 뒤 t 검정을 하자.
# 기술 통계 분석
mpg.query('fl in ["r", "p"]') \
.groupby('fl', as_index=False) \
.agg(n=('fl', 'count'),
mean=('cty', 'mean'))
| fl | n | mean | |
|---|---|---|---|
| 0 | p | 52 | 17.365385 |
| 1 | r | 168 | 16.738095 |
regular = mpg.query('fl == "r"')['cty']
premium = mpg.query('fl == "p"')['cty']
# t-test
stats.ttest_ind(regular, premium, equal_var=True)
Ttest_indResult(statistic=-1.066182514588919, pvalue=0.28752051088667036)
출력 결과를 보면 p-value가 0.05보다 큰 0.2875…이다. 실제로는 차이가 없는데 우연에 의해 이런 정도의 차이가 관찰될 확률이 28.75%라는 의미다. 따라서 ‘일반 휘발유와 고급 휘발유를 사용하는 자동차의 도시 연비 차이가 통계적으로 유의하지 않다’고 결론 내릴 수 있다. 고급 휘발유 자동차의 도시 연비 평균이 0.6 정도 높지만 이런 정도의 차이는 우연히 발생했을 가능성이 크다고 해석하는 것이다.
상관분석 - 두 변수의 관계 분석하기
상관분석correlation analysis은 두 연속 변수가 서로 관련이 있는지 검정하는 통계 분석 기법이다. 상관분석을 통해 도출한 상관계수correlation coefficient를 보면 두 변수가 얼마나 관련되어 있는지, 관련성의 정도를 파악할 수 있다. 상관계수는 0 ~ 1 사이의 값을 지니며 1에 가까울수록 관련성이 크다는 것을 의미한다. 상관계수가 양수면 정비례, 음수면 반비례 관계임을 의미한다.
실업자 수와 개인 소비 지출의 상관관계
economics 데이터를 이용해서 unemploy(실업자 수)와 pce(개인 소비 지출) 간에 상관관계가 있는지 알아보자.
1. 상관계수 구하기
상관계수는 df.corr()을 이용해 구할 수 있다. enocomics 데이터를 불러와 unemploy, pce 변수를 추출한 다음 corr()을 이용해 상관행렬을 만들자.
# economics 데이터 불러오기
economics = pd.read_csv('economics.csv')
# 상관행렬 만들기
economics[['unemploy', 'pce']].corr()
| unemploy | pce | |
|---|---|---|
| unemploy | 1.000000 | 0.614518 |
| pce | 0.614518 | 1.000000 |
출력 결과는 unemploy와 pce의 상관계수를 나타낸 행렬이다. 행과 열에 똑같은 변수가 나열되어 대칭이므로 왼쪽 아래와 오른쪽 위에 표현된 상관계수가 같다. 상관계수가 양수 0.61이므로, 실업자 수와 개인 소비 지출은 한 변수가 증가하면 다른 변수가 증가하는 정비례 관계라는 것을 알 수 있다.
2. 유의확률 구하기
df.corr()을 이용하면 상관계수를 알 수 있지만 유의확률은 알 수 없다. 유의확률은 scipy 패키지의 stats.pearsonr()을 이용해 구할 수 있다. stats.pearsonr()에 분석할 변수를 나열하면 상관계수와 유의확률을 출력한다.
# 상관분석
stats.pearsonr(economics['unemploy'], economics['pce'])
(0.6145176141932079, 6.773527303292085e-61)
출력 결과에서 첫 번째 값이 상관계수, 두 번째 값이 유의확률을 의미한다. 유의확률이 0.05 미만이므로, 실업자 수와 개인 소비 지출의 상관관계가 통계적으로 유의하다고 결론내릴 수 있다.
상관행렬 히트맵 만들기
여러 변수의 관련성을 한꺼번에 알아보고 싶을 때 모든 변수의 상관관계를 나타낸 상관행렬correlation matrix을 만들면 편리하다. 상관행렬을 보면 어떤 변수끼리 관련이 크고 적은지 한눈에 파악할 수 있다.
1. 상관행렬 만들기
mtcars 데이터를 불러와 상관행렬을 만들겠다. mtcars는 자동차 32종의 11개 변수를 담고 있다.
mtcars = pd.read_csv('mtcars.csv')
mtcars.head()
| mpg | cyl | disp | hp | drat | wt | qsec | vs | am | gear | carb | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.620 | 16.46 | 0 | 1 | 4 | 4 |
| 1 | 21.0 | 6 | 160.0 | 110 | 3.90 | 2.875 | 17.02 | 0 | 1 | 4 | 4 |
| 2 | 22.8 | 4 | 108.0 | 93 | 3.85 | 2.320 | 18.61 | 1 | 1 | 4 | 1 |
| 3 | 21.4 | 6 | 258.0 | 110 | 3.08 | 3.215 | 19.44 | 1 | 0 | 3 | 1 |
| 4 | 18.7 | 8 | 360.0 | 175 | 3.15 | 3.440 | 17.02 | 0 | 0 | 3 | 2 |
car_cor = mtcars.corr() # 상관행렬 만들기
car_cor = round(car_cor, 2) # 소수점 둘째 자리까지 반올림
car_cor
| mpg | cyl | disp | hp | drat | wt | qsec | vs | am | gear | carb | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| mpg | 1.00 | -0.85 | -0.85 | -0.78 | 0.68 | -0.87 | 0.42 | 0.66 | 0.60 | 0.48 | -0.55 |
| cyl | -0.85 | 1.00 | 0.90 | 0.83 | -0.70 | 0.78 | -0.59 | -0.81 | -0.52 | -0.49 | 0.53 |
| disp | -0.85 | 0.90 | 1.00 | 0.79 | -0.71 | 0.89 | -0.43 | -0.71 | -0.59 | -0.56 | 0.39 |
| hp | -0.78 | 0.83 | 0.79 | 1.00 | -0.45 | 0.66 | -0.71 | -0.72 | -0.24 | -0.13 | 0.75 |
| drat | 0.68 | -0.70 | -0.71 | -0.45 | 1.00 | -0.71 | 0.09 | 0.44 | 0.71 | 0.70 | -0.09 |
| wt | -0.87 | 0.78 | 0.89 | 0.66 | -0.71 | 1.00 | -0.17 | -0.55 | -0.69 | -0.58 | 0.43 |
| qsec | 0.42 | -0.59 | -0.43 | -0.71 | 0.09 | -0.17 | 1.00 | 0.74 | -0.23 | -0.21 | -0.66 |
| vs | 0.66 | -0.81 | -0.71 | -0.72 | 0.44 | -0.55 | 0.74 | 1.00 | 0.17 | 0.21 | -0.57 |
| am | 0.60 | -0.52 | -0.59 | -0.24 | 0.71 | -0.69 | -0.23 | 0.17 | 1.00 | 0.79 | 0.06 |
| gear | 0.48 | -0.49 | -0.56 | -0.13 | 0.70 | -0.58 | -0.21 | 0.21 | 0.79 | 1.00 | 0.27 |
| carb | -0.55 | 0.53 | 0.39 | 0.75 | -0.09 | 0.43 | -0.66 | -0.57 | 0.06 | 0.27 | 1.00 |
출력된 상관행렬을 보면 mtcars의 변수들이 서로 얼마나 관련되는지 알 수 있다.
-
mpg(연비) 행과 cyl(실린더 수) 열이 교차되는 부분을 보면 상관계수가 -0.85이므로, 연비가 높을수록 실린더 수가 적은 경향이 있다.
-
cyl(실린더 수)과 wt(무게)의 상관계수가 0.78이므로, 실린더 수가 많을수록 자동차가 무거운 경향이 있다.
2. 히트맵 만들기
여러 변수로 상관행렬을 만들면 출력된 값이 너무 많아서 관심있는 변수들의 관계를 파악하기 어렵다. 이럴 때 값의 크기를 색깔로 표현한 히트맵heatmap을 만들면 변수들의 관계를 쉽게 파악할 수 있다. seaborn 패키지의 heatmap()을 이용하면 상관행렬로 히트맵을 만들 수 있다.
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.dpi': '120', # 해상도 설정
'figure.figsize': [7.5, 5.5]}) # 가로 세로 크기 설정
# 히트맵 만들기
import seaborn as sns
sns.heatmap(car_cor,
annot=True, # 상관계수 표시
cmap='RdBu'); # 컬러맵
히트맵은 상관계수가 클수록 상자 색깔을 진하게 표현하고, 상관계수가 양수면 파란색, 음수면 빨간색 계열로 표현한다. 상자 색깔을 보면 상관관계의 정도와 방향을 쉽게 파악할 수 있다.
대각 행렬 제거하기
상관행렬은 행과 열에 같은 변수가 나열되므로 앞에서 만든 히트맵은 대각선 기준으로 왼쪽 아래와 오른쪽 위의 값이 대칭하여 중복된다. sns.heatmap()의 mask를 이용해 중복된 부분을 제거하겠다.
(1) mask 만들기
np.zeros_like()를 이용해 상관행렬의 행과 열의 수 만큼 0으로 채운 배열array을 만든다.
# mask 만들기
import numpy as np
mask = np.zeros_like(car_cor)
mask
array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
배열의 오른쪽 위 인덱스index를 구하는 np.triu_indices_from()를 활용해 mask의 오른쪽 위 대각 행렬을 1로 바꾼다.
# 오른쪽 위 대각 행렬을 1로 바꾸기
mask[np.triu_indices_from(mask)] = 1
mask
array([[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[0., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[0., 0., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[0., 0., 0., 1., 1., 1., 1., 1., 1., 1., 1.],
[0., 0., 0., 0., 1., 1., 1., 1., 1., 1., 1.],
[0., 0., 0., 0., 0., 1., 1., 1., 1., 1., 1.],
[0., 0., 0., 0., 0., 0., 1., 1., 1., 1., 1.],
[0., 0., 0., 0., 0., 0., 0., 1., 1., 1., 1.],
[0., 0., 0., 0., 0., 0., 0., 0., 1., 1., 1.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 1., 1.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]])
(2) 히트맵에 mask 적용하기
sns.heatmap()에 mask를 적용한다. 출력된 히트맵을 보면 mask의 1에 해당하는 위치의 값이 제거되어 왼쪽 아래의 상관계수만 표현된다.
# 히트맵 만들기
sns.heatmap(data=car_cor,
annot=True, # 상관계수 표시
cmap='RdBu', # 컬러맵
mask=mask); # mask 적용
(3) 빈 행과 열 제거하기
앞에서 만든 히트맵의 왼쪽 위 mpg 행과 오른쪽 아래 carb 열에는 아무 값도 표현되어 있지 않다. 행과 열의 변수가 같아서 상관계수가 항상 1이 되는 위치이므로 값을 표현하지 않은 것이다. 히트맵의 빈 행과 열을 제거하려면 mask와 상관행렬의 첫 번째 행과 마지막 열을 제거한 다음 히트맵을 만들면 된다.
mask_new = mask[1:, :-1] # mask 첫 번째 행, 마지막 열 제거
cor_new = car_cor.iloc[1:, :-1] # 상관행렬 첫 번째 행, 마지막 열 제거
# 히트맵 만들기
sns.heatmap(data=cor_new,
annot=True, # 상관계수 표시
cmap='RdBu', # 컬러맵
mask=mask_new); # mask 적용
파라미터를 몇 가지 추가해 히트맵을 보기 좋게 수정해보자. 출력된 히트맵을 보면 변수 간의 관계를 쉽게 알 수 있다.
# 히트맵 만들기
sns.heatmap(data=cor_new,
annot=True, # 상관계수 표시
cmap='RdBu', # 컬러맵
mask=mask_new, # mask 적용
linewidths=.5, # 경계 구분선 추가
vmax=1, # 가장 진한 파란색으로 표현할 최대값
vmin=-1, # 가장 진한 빨간색으로 표현할 최소값
cbar_kws={"shrink": .5}); # 범례 크기 줄이기
sns.heatmap()의 파라미터를 이용하면 히트맵의 모양을 다양하게 바꿀 수 있다. seaborn 공식 문서를 참고하자.
- seaborn.heatmap: bit.ly/easypy_142
머신러닝을 이용한 예측 분석
머신러닝 모델 알아보기
머신러닝 모델이 무엇인지, 머신러닝 모델을 이용해 어떻게 예측을 하는지 알아보자.
머신러닝 모델이란?
머신러닝 모델 만들기 = 함수 만들기
머신러닝 모델은 함수와 비슷하다. 함수에 값을 입력하면 규칙에 따라 계산한 값을 출력하듯이 머신러닝 모델도 값을 입력하면 정해진 규칙에 따라 계산한 예측값을 출력한다. 머신러닝 모델이 함수와 다른 점은 만드는 방법이다. 함수를 만들 때는 사람이 계산 규칙을 정해 입력해야 하지만 머신러닝 모델을 만들 때는 사람이 계산 규칙을 정하지 않고 컴퓨터가 데이터에서 패턴을 찾아 스스로 규칙을 정하게 한다.
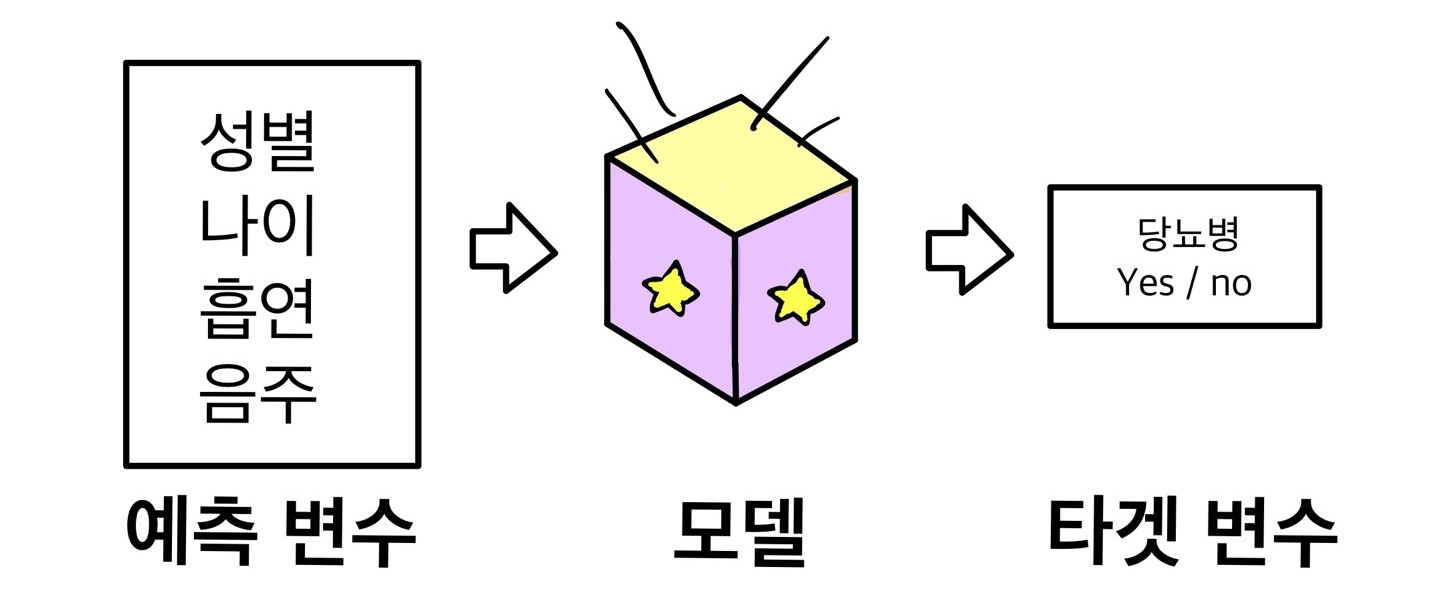
예를 들어 환자의 정보를 입력받아 당뇨병 발병 여부를 예측하는 모델을 만든다면, 사람이 해야 할 일은 여러 환자의 정보와 당뇨병 발병 여부 데이터를 수집해 머신러닝 알고리즘에 입력하는 것뿐이다. 그러면 컴퓨터는 환자의 정보와 당뇨병 발병 간의 패턴을 찾아낸 다음 환자의 정보를 입력하면 당뇨병 발병 여부를 출력하는 모델을 만든다. 어떤 사람의 당뇨병 발병 여부를 알고 싶다면 환자의 정보를 모델에 입력하기만 하면 된다.
예측 변수와 타겟 변수
머신러닝 모델을 만들 때 두 종류의 변수를 사용한다.
-
예측 변수(predictor variable): 예측하는 데 활용하는 변수 또는 모델에 입력하는 값을 예측 변수라 한다.
-
타겟 변수(target variable): 예측하고자 하는 변수 또는 모델이 출력하는 값을 타겟 변수라 한다.
만약 환자의 성별, 나이, 흡연 여부, 음주 여부로 당뇨병 발병을 예측하는 모델을 만든다면 성별, 나이, 흡연 여부, 음주 여부는 예측 변수로 사용하고, 당뇨병 발병 여부는 타겟 변수로 사용한다.
머신러닝 모델을 이용해 미래 예측하기
머신러닝 모델은 미래의 값을 예측하는 용도로 자주 사용된다. 과거의 값을 예측 변수로 사용하고 미래의 값을 타겟 변수로 사용하면 미래를 예측하는 모델을 만들 수 있다. 예를 들어 현재 환자의 신체 정보를 입력하면 3년 뒤의 당뇨병 발병 여부를 예측하는 모델을 만들 수 있다.
머신러닝 모델은 다양한 사업 영역에서 미래를 예측하는 데 활용된다. 온라인 커머스는 고객이 구매할 가능성이 높은 상품을 예측해 추천하고, 마케팅사는 서비스에 가입할 가능성이 높은 이용자를 예측해 홍보 전화를 건다. 금융사는 고객이 대출금을 제때 상환할지 예측해 가입 승인 여부를 결정하고, 반도체 공장은 설비 고장을 예측해 설비가 고장 나기 전에 미리 정비한다. 미래를 예측하면 부가 수익을 창출하고 비용을 줄일 수 있으므로 머신러닝은 여러 분야에서 주목받는 기술이다.
의사결정나무 모델
머신러닝 모델은 종류가 매우 다양하고 새로운 알고리즘이 끊임없이 개발되고 있다. 그 중에서 의사결정나무 모델은 구조가 단순하고 작동 원리를 이해하기 쉬워 여러 분야에 사용되고 있다. 규모가 크고 복잡한 모델도 의사결정나무 모델에 기반을 두고 만들 때가 많다.
의사결정나무 모델이란?
의사결정나무decision tree모델은 마치 스무고개 놀이처럼 순서대로 주어진 질문에 yes/no로 답하면서 마지막에 결론을 얻는 구조로 되어 있다. 질문이 나열된 모양이 가지를 뻗은 ‘나무’와 비슷하고, 예측값을 무엇으로 할지 ‘의사 결정’해 주기 때문에 의사결정나무라는 이름을 가지고 있다.
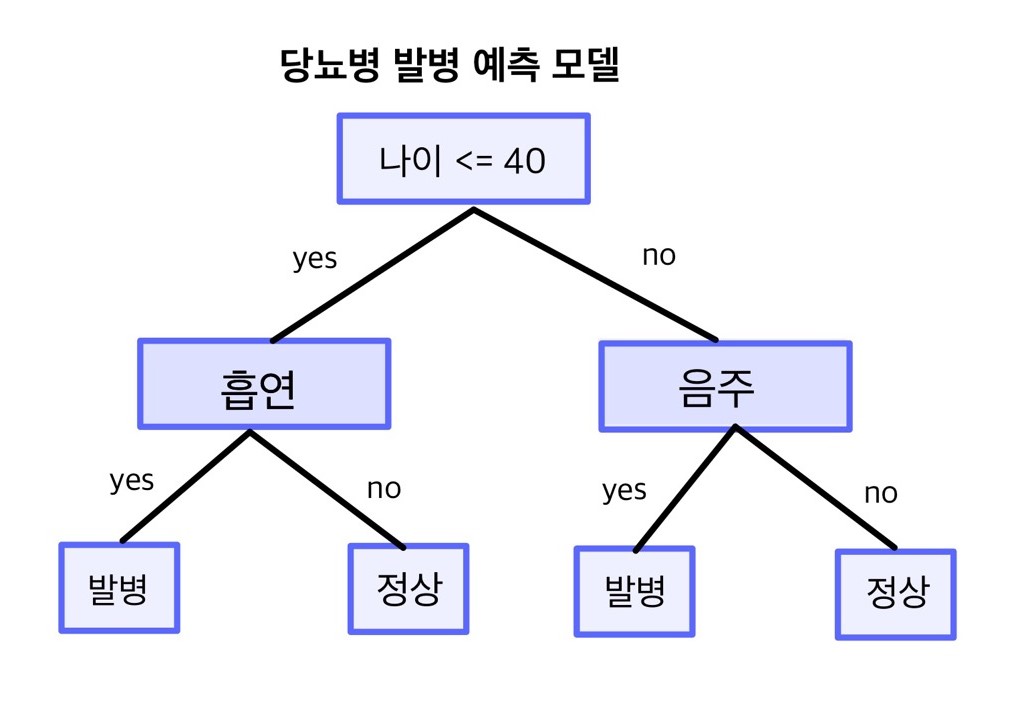
의사결정나무 모델을 이용해 예측하기
의사결정나무 모델을 만들면 yes/no로 답할 수 있는 질문 목록을 갖게 된다. 새 데이터가 주어졌을 때 질문 목록에 따라 순서대로 답을 하면 최종적으로 둘 중 한 가지 값을 부여받게 된다. 예를 들어 환자의 나이, 흡연 여부, 음주 여부로 당뇨병 발병 여부를 예측하는 모델을 만들었다고 해보자.
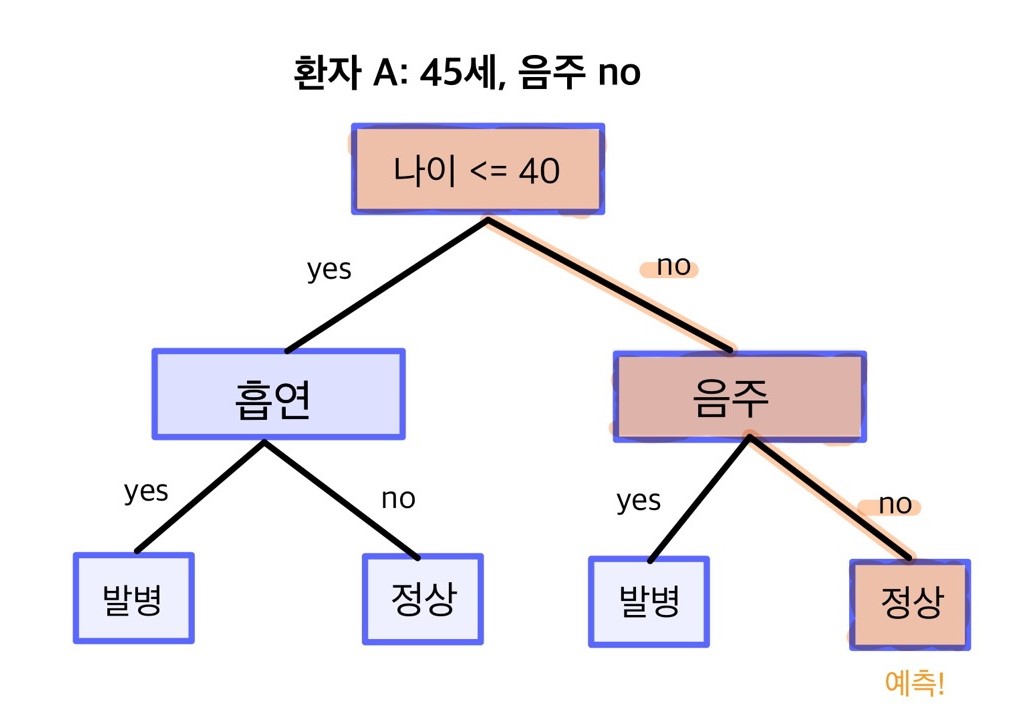
새로 온 환자 A는 나이가 45세이고 음주는 하지 않는다. 모델의 첫 번째 질문은 ‘나이가 40세 이하인가?’이다. 이 질문에 A의 대답은 ‘no’이므로 오른쪽 가지를 타고 내려간다. 두 번째로 마주한 질문 ‘음주 여부’에 A의 대답은 ‘no’이므로 이번에도 오른쪽 가지를 타고 내려간다. 최종적으로 환자 A는 ‘정상’으로 예측된다.
두 번째 환자 B는 나이가 30세이고 흡연을 한다. B는 40세 이하이니 첫 번째 질문의 대답이 ‘yes’이므로 왼쪽 가지를 타고 내려간다. 두 번째로 마주한 질문 ‘흡연 여부’의 대답은 ‘yes’이므로 왼쪽 가지를 타고 내려간다. 최종적으로 환자 B는 ‘발병’으로 예측된다. 이처럼 데이터에 모델의 질문에 답할 수 있는 값만 있으면 발병/정상 둘 중 한 가지로 예측값을 부여받게 된다.
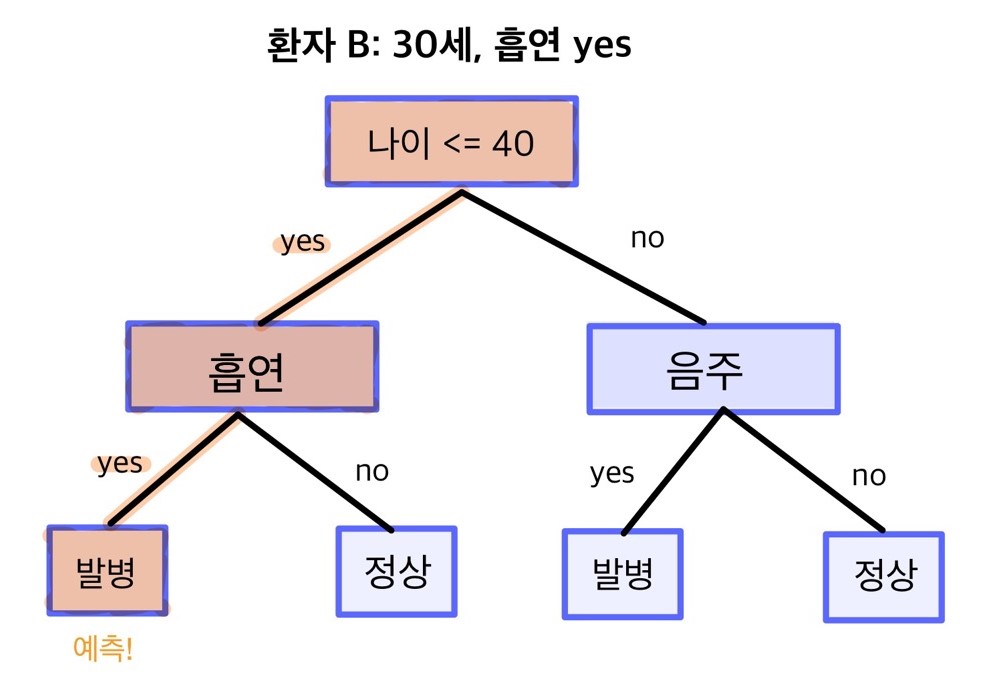
발병/정상처럼 둘 중 한 가지 값으로 분류하는 모델을 이진 분류 모델(binary classification model)이라고 한다. 의사결정나무 모델을 이용하면 셋 이상의 값으로 분류하는 다중 분류 모델(multiclass classification model)도 만들 수 있다.
의사결정나무 모델이 만들어지는 원리
다음과 같이 4가지 예측 변수로 당뇨병 발병 여부를 예측하는 모델을 만든다고 가정하고 모델이 만들어지는 과정을 단계별로 살펴보자.
-
예측 변수: 흡연 여부, 음주 여부, 성별, 나이
-
타겟 변수: 당뇨병 발병 여부
1단계. 타겟 변수를 가장 잘 분리하는 예측 변수 선택하기
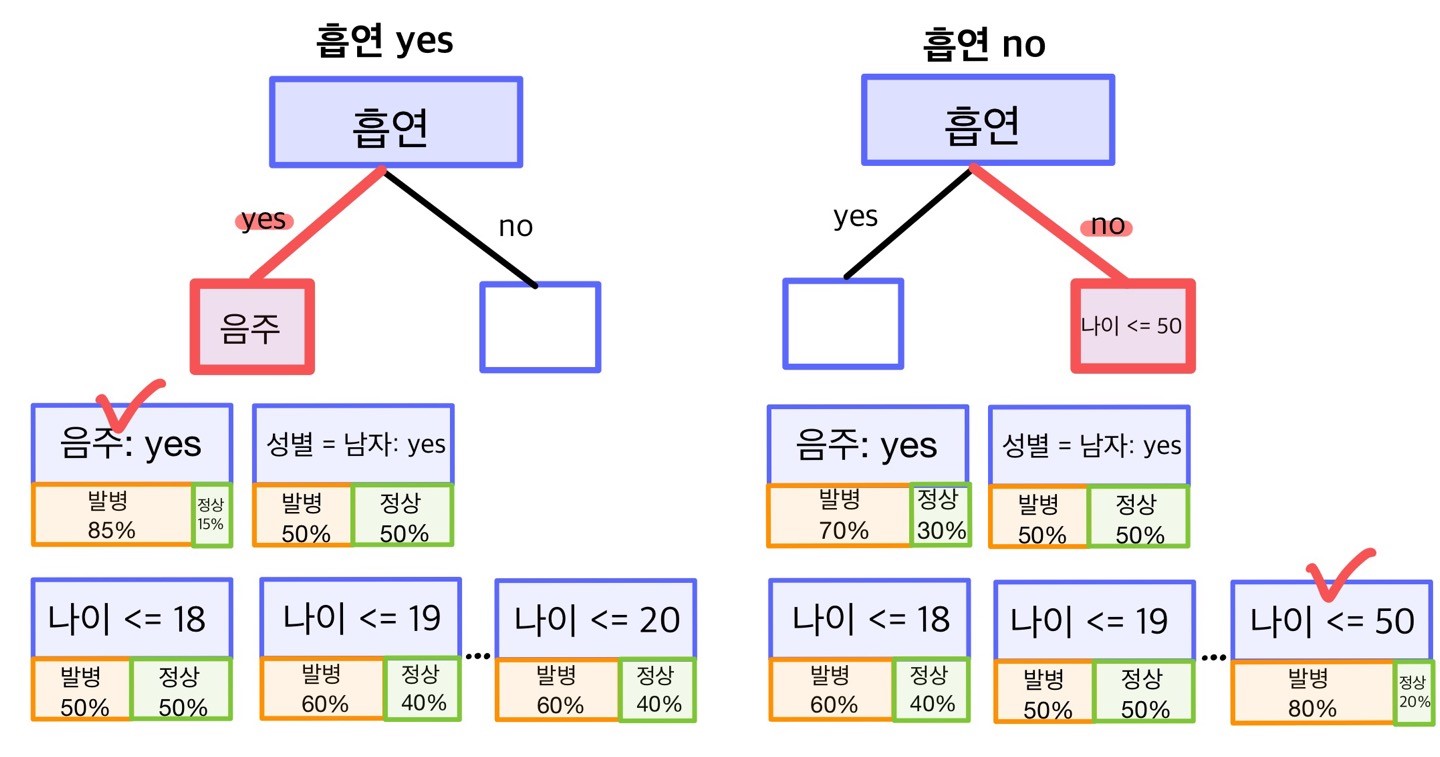
의사결정나무 모델은 어떤 순서로 어떤 질문을 할지 정하는 과정을 거쳐 만들어진다. 가장 먼저 첫 번째 질문을 할 때 예측 변수 중에서 무엇을 사용할지 정한다. 의사결정나무 알고리즘은 ‘타겟 변수를 가장 잘 분리해 주는 예측 변수’를 찾아 첫 번째 질문으로 삼는다. 예측 변수가 타겟 변수를 분리해 주는 정도는 다음 절차로 알 수 있다.
-
모든 예측 변수를 yes/no로 답할 수 있는 질문으로 만든다. ‘흡연 여부’는 ‘흡연을 하십니까?’, ‘음주 여부’는 ‘음주를 하십니까?’, ‘성별’은 ‘남자입니까?’ 또는 ‘여자입니까?’의 형태로 만든다.
-
모델을 만드는데 사용할 데이터를 앞에서 만든 각각의 질문에 대입한 다음 ‘yes’로 답한 데이터만 추출한다.
-
추출한 데이터 중 발병인과 정상인의 비율을 구한다. 발병인과 정상인의 비율 차이가 크면 클수록 예측 변수가 타겟 변수를 잘 분리해낸다고 볼 수 있다.

앞의 그림을 보면 ‘성별 = 남자’는 ‘yes’로 답한 사람 중 발병과 정상의 비율이 둘 다 50%로 같다. 그러므로 성별을 묻는 것은 발병과 정상을 분리해 내는데 별로 도움이 되지 않는다.
반면 ‘음주 여부’는 성별 보다 발병과 정상을 잘 분리해 낸다. 음주 여부에 ‘yes’로 답한 사람을 전부 환자로 분류하면 적어도 60%는 맞출 수 있다.
셋 중에 타겟 변수를 가장 잘 분리해 주는 예측 변수는 ‘흡연 여부’이다. 흡연 여부에 ‘yes’로 답한 사람을 전부 환자로 분류하면 80%를 맞출 수 있다. 만약 당뇨병 발병 여부를 예측하는 데 질문을 딱 하나만 해야 한다면 흡연 여부를 물어봐야 한다.
앞에서 살펴본 변수는 범주 변수이므로 yes/no로 답할 수 있는 질문을 곧바로 만들 수 있지만 나이와 같은 연속 변수는 그렇지 않다. 연속 변수는 ‘나이가 x세 이하인가?’의 형태로 질문을 만들어야 yes/no로 답할 수 있다. 이때 몇 세를 기준으로 질문할지 정해야한다. 타겟 변수를 가장 잘 분리해 주는 기준 나이를 알아내려면 ‘18세 이하인가?’, ‘19세 이하인가?’, …, ‘60세 이하인가?’와 같이 가능한 모든 경우의 수대로 질문 후보를 만들어 비교하면 된다.

이처럼 모든 예측 변수로 질문을 만든 다음 타겟 변수를 가장 잘 분리해 주는 변수를 찾아 첫 번째 질문에 사용한다. 이 예에서는 흡연 여부를 선택하게 된다.
실제 계산에서는 노드 분리 전후를 비교하여 지니 계수(gini index)나 엔트로피(entropy)와 같은 불순도(impurity)를 가장 줄여주는 예측 변수를 선택한다.

2단계. 첫 번째 질문의 답변에 따라 데이터를 두 노드로 분할하기
질문의 답변이 같아서 함께 분류된 집단을 노드node라고 한다. 노드는 의사결정나무 도식에 사각형으로 표현된다.
전체 데이터를 첫 번째 질문의 답변에 따라 서로 다른 노드로 보낸다. 앞의 예에서는 ‘흡연 여부’의 답변이 ‘yes’면 왼쪽 노드, ‘no’면 오른쪽 노드로 보내면 된다.
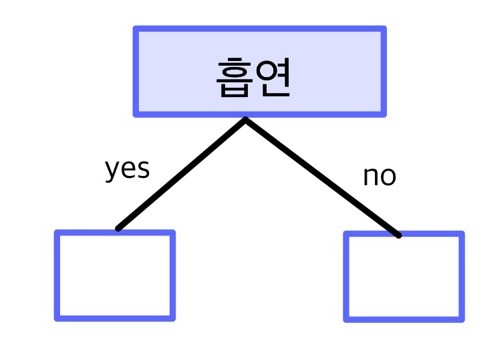
3단계. 각 노드에서 타겟 변수를 가장 잘 분리하는 예측 변수 선택하기
각 노드에서 타겟 변수를 가장 잘 분리해 주는 예측 변수를 선택한다. 1단계 작업을 노드별로 반복하는 것이다. ‘흡연 여부’는 이미 사용했으니 제외하고 나머지 변수 중에서 타겟 변수를 가장 잘 분리해 주는 두 번째 예측 변수를 찾으면 된다.
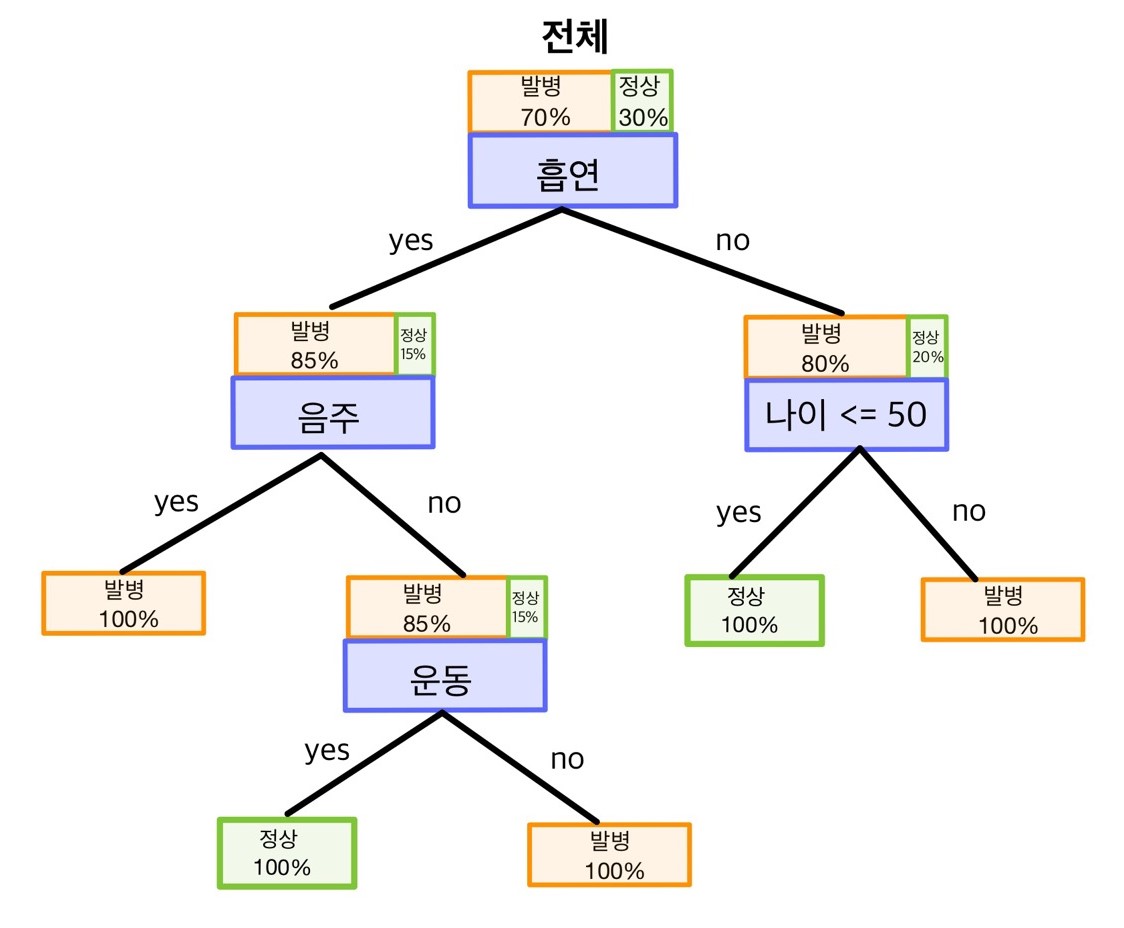
4단계. 노드가 완벽하게 분리될 때까지 반복하기
노드에 한 범주만 남아 완벽하게 분리될 때까지 변수를 선택하고 노드를 분할하는 과정을 반복한다. 노드에 발병과 정상 중 한 쪽 범주만 남으면 분할을 종료한다.
의사결정나무 모델의 특징
- 노드마다 분할 횟수가 다르다
예측 변수를 선택하고 노드를 분할하는 횟수가 노드마다 다르므로 가지가 뻗어 나간 횟수도 노드마다 제각각이다. 어떤 노드는 다섯 번 분할해야 한 범주만 남지만 어떤 노드는 두 번만에 한 범주만 남을 수 있다. 따라서 모든 사람에게 같은 횟수로 질문하는 게 아니라 앞의 질문에 어떻게 답변했는지에 따라 서로 다른 횟수로 질문하게 된다.
- 노드마다 선택되는 예측 변수가 다르다
예측 변수 선택 작업을 노드별로 따로 하므로 노드마다 선택되는 변수가 다르다. 예를 들어 흡연자에게는 ‘음주 여부’가, 비흡연자에게는 ‘나이’가 타겟 변수를 가장 잘 분리해 주는 예측 변수일 수 있다. 따라서 모든 사람에게 일괄적으로 같은 질문을 하는 게 아니라 앞의 질문에 어떻게 답변했는지에 따라 서로 다른 질문을 하게 된다.
- 어떤 예측 변수는 모델에서 탈락한다
어떤 예측 변수는 노드를 분할하는 과정에서 한 번도 선택되지 않아 모델에서 탈락할 수 있다. 예를 들어 당뇨병 발병 예측 모델을 만들 때 ‘발 크기’ 변수는 타겟 변수를 분리해 주는 정도가 다른 변수보다 항상 떨어져서 분할을 종료할 때까지 한 번도 선택되지 않을 수 있다. 따라서 데이터에 들어 있는 모든 변수를 예측에 사용하는 게 아니라 일부는 사용하고 일부는 제외하게 된다.
소득 예측 모델 만들기
adult 데이터는 미국인의 성별, 인종, 직업, 학력 등 다양한 인적 정보를 담고 있는 인구 조사 데이터다. adult 데이터를 이용해 인적 정보로 소득을 예측하는 의사결정나무 모델을 만들어보자. 모델을 만드는 절차는 다음과 같다.
먼저 adult 데이터를 불러와 구조를 살펴보겠다.
import pandas as pd
df = pd.read_csv('adult.csv')
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 48842 entries, 0 to 48841 Data columns (total 15 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 age 48842 non-null int64 1 workclass 48842 non-null object 2 fnlwgt 48842 non-null int64 3 education 48842 non-null object 4 education_num 48842 non-null int64 5 marital_status 48842 non-null object 6 occupation 48842 non-null object 7 relationship 48842 non-null object 8 race 48842 non-null object 9 sex 48842 non-null object 10 capital_gain 48842 non-null int64 11 capital_loss 48842 non-null int64 12 hours_per_week 48842 non-null int64 13 native_country 48842 non-null object 14 income 48842 non-null object dtypes: int64(6), object(9) memory usage: 5.6+ MB
adult 데이터는 48,842명의 정보를 담고 있으며 변수 15개로 구성된다. 이 중 연소득을 나타낸 income을 타겟 변수, 나머지 14개를 예측 변수로 사용하겠다.
| 변수명 | 의미 |
|---|---|
| age | 나이 |
| workclass | 근로 형태 |
| fnlwgt | 인구 통계 가중치 |
| education | 최종 학력 |
| education_num | 교육 기간 |
| marital_status | 결혼 상태 |
| occupaction | 직종 |
| relationship | 가구주와의 관계 |
| race | 인종 |
| sex | 성별 |
| capital_gain | 자본 소득(USD) |
| capital_loss | 자본 손실(USD) |
| hours_per_week | 주당 근무 시간 |
| native_country | 출신 국가 |
| income | 연소득 |
소득 예측 모델을 어디에 활용할까?
- 고가 상품 구매 프로모션
소득 예측 모델은 고급 수입차나 명품 시계처럼 고가의 상품을 구매하도록 독려하는 프로모션에 활용할 수 있다. 소득이 높아 상품을 구매할 가능성이 높은 사람을 예측하면 프로모션 활동에 드는 시간과 비용을 절약할 수 있다.
- 저소득층 지원 대상 확대
정부에서 저소득층 지원 사업 대상자를 찾아낼 때에도 소득 예측 모델을 활용할 수 있다. 저소득층을 선제적으로 찾아 지원하면 사람들이 스스로 지원 요건을 확인하고 신청하게 할 때보다 복지 프로그램 대상을 확대할 수 있다.
전처리하기
머신러닝 모델을 만들 때 가장 먼저 하는 작업은 모델을 만드는 데 적합하도록 데이터를 가공하는 것이다. 본격적으로 모델을 만들기 전에 데이터를 처리하는 작업이므로 이를 데이터 전처리data preprocessing라 한다. adult 데이터를 전처리하겠다.
1. 타겟 변수 전처리
먼저 타겟 변수 income을 검토하고 전처리하겠다. income은 조사 응답자의 연소득이 5만 달러를 초과하는지 여부를 나타낸다. 다음 코드의 출력 결과를 보면 연소득이 5만 달러를 초과하는 사람(>50K)은 23.9%, 5만 달러 이하인 사람(<=50K)은 76%이다.
import numpy as np
np.round((df['income'].value_counts(normalize=True) * 100), 2).astype(str) + '%'
<=50K 76.07% >50K 23.93% Name: income, dtype: object
변수의 값에 특수 문자나 대소문자가 섞여 있으면 다루기 불편하므로 5만 달러를 초과하면 ‘high’, 그렇지 않으면 ‘low’로 값을 수정한다.
df['income'] = np.where(df['income'] == '>50K', 'high', 'low')
np.round((df['income'].value_counts(normalize=True) * 100), 2).astype(str) + '%'
low 76.07% high 23.93% Name: income, dtype: object
2. 불필요한 변수 제거하기
이름, 아이디, 주소 같은 변수는 대부분의 값이 고유값이어서 반복되는 패턴이 없고 타겟 변수와도 관련성이 없다. 이런 변수는 타겟 변수를 예측하는 데 도움이 되지 않고 모델링 시간만 늘리는 역할을 하므로 제거해야 한다.
fnlwgt는 adult 데이터를 이용해 미국의 실제 인구를 추정할 때 사용하는 가중치다. 인종, 성별, 나이 등 인구 통계 속성이 같으면 fnlwgt가 같다. fnlwgt는 타겟 변수를 예측하는 데 도움이 되지 않는 변수이므로 모델을 만들 때 사용하지 않도록 제거한다.
df = df.drop(columns='fnlwgt')
3. 문자 타입 변수를 숫자 타입으로 바꾸기
모델을 만드는 데 사용되는 모든 변수는 숫자 타입이어야 한다. df.info()의 출력 결과를 보면 Dtype이 object인 문자 타입 변수들이 있다. 이 변수들을 모델을 만드는 데 활용하려면 숫자 타입으로 바꾸어야 한다.
원핫 인코딩하기
변수의 범주가 특정 값이면 1, 그렇지 않으면 0으로 바꾸면 문자 타입 변수를 숫자 타입으로 만들 수 있다. 이렇게 값을 1과 0으로 바꾸는 방법을 원핫 인코딩one-hot encoding이라 한다.
다음 표를 밑의 형식으로 바꾼다.
| 동물 |
|---|
| 강아지 |
| 앵무새 |
| 고양이 |
| 앵무새 |
| 강아지 |
| 고양이 |
| 강아지 | 고양이 | 앵무새 |
|---|---|---|
| 1 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
df의 sex를 추출해 원핫 인코딩하는 방법을 알아보자. 다음 코드의 출력 결과를 보면 df_tmp의 sex는 ‘Male’ 또는 ‘Female’로 되어 있는 문자 타입 변수이다.
df_tmp = df[['sex']]
df_tmp.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 48842 entries, 0 to 48841 Data columns (total 1 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 sex 48842 non-null object dtypes: object(1) memory usage: 381.7+ KB
df_tmp['sex'].value_counts()
Male 32650 Female 16192 Name: sex, dtype: int64
pd.get_dummies()에 데이터프레임을 입력하면 문자 타입 변수를 원핫 인코딩을 적용해 변환한다. 다음 코드의 출력 결과를 보면 sex가 사라지고 그 대신 sex_Female과 sex_Male이 만들어졌다.
# df_tmp의 문자 타입 변수에 원핫 인코딩 적용
df_tmp = pd.get_dummies(df_tmp)
df_tmp.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 48842 entries, 0 to 48841 Data columns (total 2 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 sex_Female 48842 non-null uint8 1 sex_Male 48842 non-null uint8 dtypes: uint8(2) memory usage: 95.5 KB
참고로 원핫 인코딩으로 만들어진 변수의 타입은 uint8로 0 ~ 255의 양수를 담을 수 있는 데이터 타입이다.
sex_Female은 sex가 Female이면 1, 그렇지 않으면 0으로 된 변수다. sex_Male은 반대로 sex가 Male이면 1, 그렇지 않으면 0으로 된 변수다. 두 변수 중 한쪽이 1이면 다른 한쪽은 반드시 0이다.
df_tmp[['sex_Female', 'sex_Male']].head()
| sex_Female | sex_Male | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 0 | 1 |
| 4 | 1 | 0 |
원핫 인코딩을 하는 방법을 익혔으니 df에 적용하겠다. 타겟 변수인 income만 원래대로 유지하고, 모든 문자 타입 변수를 원핫 인코딩하자.
target = df['income'] # income 추출
df = df.drop(columns='income') # income 제거
df = pd.get_dummies(df) # 문자 타입 변수 원핫 인코딩
df['income'] = target # df에 target 삽입
df.info()
<class 'pandas.core.frame.DataFrame'> RangeIndex: 48842 entries, 0 to 48841 Columns: 108 entries, age to income dtypes: int64(5), object(1), uint8(102) memory usage: 7.0+ MB
df.inco() 출력 결과에 개별 변수의 정보가 출력되지 않은 이유는 변수가 100개 이하일 때만 변수 정보를 출력하도록 설정되어 있기 때문이다. df.info()에 max_cols=np.inf를 입력하면 변수의 수와 관계없이 모든 변수의 정보를 출력한다. 출력 결과를 보면 변수가 108개로 늘어나고, 문자 타입 변수가 전부 숫자 타입으로 바뀌었다는 것을 알 수 있다.
df.info(max_cols=np.inf)
<class 'pandas.core.frame.DataFrame'> RangeIndex: 48842 entries, 0 to 48841 Data columns (total 108 columns): # Column Non-Null Count Dtype --- ------ -------------- ----- 0 age 48842 non-null int64 1 education_num 48842 non-null int64 2 capital_gain 48842 non-null int64 3 capital_loss 48842 non-null int64 4 hours_per_week 48842 non-null int64 5 workclass_? 48842 non-null uint8 (...생략...)
4. 데이터 분할하기
모델을 만들 때는 가지고 있는 모든 데이터를 사용하는 게 아니라 일부만 무작위로 추출해 사용해야 한다.
모든 데이터를 사용해 모델을 만들면 성능 평가 점수를 신뢰할 수 없다
모델을 만들고 나면 모델이 타겟 변수를 얼마나 정확하게 예측하는지 알아보기 위해 성능을 평가한다. 그런데 모델을 만들 때 사용한 데이터를 성능을 평가할 때 그대로 다시 사용하면 평가 점수를 신뢰할 수 없게 된다. 예측 정확도가 높게 나오더라도 모델의 성능이 좋아서인지 아니면 이미 경험한 데이터라 잘 맞춘 것인지 알 수 없기 때문이다.
이는 학생이 연습 문제로 공부한 다음 똑같은 문제로 시험을 치르는 상황과 비슷하다. 공부할 때 풀어본 문제를 다시 푸는 것에 불과하므로 실력을 제대로 평가할 수 없는 것이다.
크로스 밸리데이션: 신뢰할 수 있는 성능 평가 점수를 얻는 방법
신뢰할 수 있는 성능 평가 점수를 얻으려면 가지고 있는 데이터에서 일부만 추출해 모델을 만들 때 사용하고, 나머지는 남겨 두었다가 성능을 평가할 때 사용해야 한다. 다음 그림처럼 데이터를 훈련용과 평가용으로 나누어 사용하는 것이다. 이렇게 하면 모델이 한 번도 경험한 적 없는 데이터로 성능을 평가하므로 평가 점수를 신뢰할 수 있게 된다.
이는 학생이 문제 은행에서 일부만 뽑아 공부한 다음 나머지 문제로 시험을 치르는 상황과 비슷하다. 공부할 때 이미 풀어본 문제가 아니라 처음 보는 문제를 얼마나 잘 푸는 지 봐야만 실력을 제대로 평가할 수 있는 것이다.
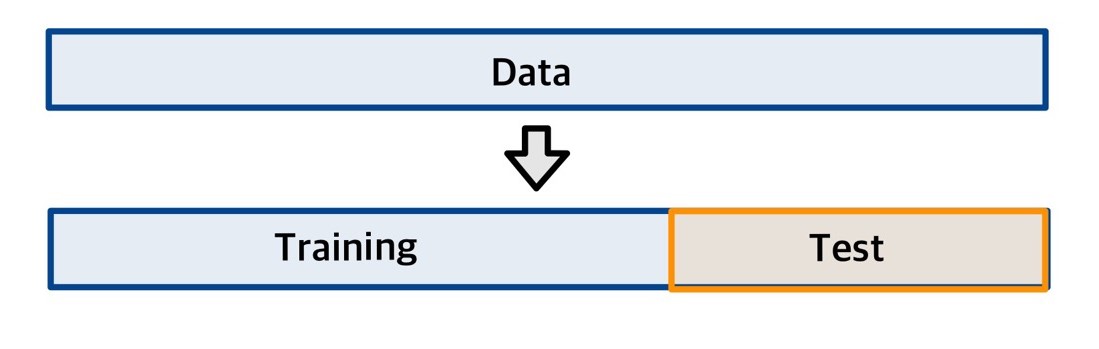
이처럼 데이터를 분할해 일부는 모델을 만들 때 사용하고 나머지는 평가할 때 사용하는 방법을 크로스 밸리데이션(cross validation, 교차 검증)이라고 한다. 분할한 데이터 중에서 모델을 만들 때 사용하는 데이터를 트레이닝 세트(training set, 훈련 세트), 성능을 평가할 때 사용하는 데이터를 테스트 세트(test set, 시험 세트)라 부른다. 또한, 모델을 만드는 작업을 ‘training’이라고 표현하고 우리말로는 ‘훈련’ 또는 ‘학습’으로 번역한다.
adult 데이터 분할하기
scikit-learn 패키지를 이용해 데이터를 트레이닝 세트와 테스트 세트로 분할하겠다. scikit-learn은 머신러닝 모델을 만들 때 가장 많이 사용되는 패키지다.
sklearn.model_selection의 train_test_split()을 이용하면 데이터를 트레이닝 세트와 테스트 세트로 분할할 수 있다. train_test_split()에는 다음과 같은 파라미터를 입력해야 한다.
-
test_size: 테스트 세트의 비율. 트레이닝 세트와 테스트 세트의 비율은 보통 7:3 또는 8:2로 정한다. 정답은 없지만 데이터가 많을수록 트레이닝 세트의 비율을 늘리고 반대로 데이터가 적을수록 테스트 세트의 비율을 늘린다.
-
stratify: 범주별 비율을 통일할 변수. stratify에 타겟 변수를 입력하면 트레이닝 세트와 테스트 세트에 타겟 변수의 범주별 비율을 비슷하게 맞춰준다. 타겟 변수를 입력하지 않으면 타겟 변수의 범주별 비율이 데이터 세트마다 달라지므로 평가 결과를 신뢰하기 어렵다.
-
random_state: 난수 초깃값.
train_test_split()은 난수를 이용해 데이터를 무작위로 추출하므로 함수를 실행할 때마다 추출되는 데이터가 조금씩 달라진다. 난수를 고정하면 코드를 반복 실행해도 항상 같은 데이터가 추출된다.
다음 코드는 함수의 출력 결과를 df_train, df_test 두 변수에 할당하는 형태로 되어 있다. train_test_split()은 트레이닝 세트와 테스트 세트를 함께 출력한다. 할당할 변수를 2개 지정하면 트레이닝 세트는 앞에 입력한 변수, 테스트 세트는 뒤에 입력한 변수에 할당한다.
from sklearn.model_selection import train_test_split
df_train, df_test = train_test_split(df,
test_size=0.3, # 테스트 세트 비율
stratify=df['income'], # 타겟 변수 비율 유지
random_state=1234) # 난수 고정
df.shape로 두 데이터 세트를 살펴보면 변수가 108개로 같고, 행의 수는 다르다.
# train
df_train.shape
(34189, 108)
# test
df_test.shape
(14653, 108)
타겟 변수의 범주별 비율은 두 데이터 세트 모두 비슷하다. train_test_split()의 stratify에 타겟 변수를 지정했기 때문이다.
# train
df_train['income'].value_counts(normalize=True)
low 0.760713 high 0.239287 Name: income, dtype: float64
# test
df_test['income'].value_counts(normalize=True)
low 0.760732 high 0.239268 Name: income, dtype: float64
의사결정나무 모델 만들기
전처리를 완료했으니 이제 모델을 만들어보자. 모델을 만들 때는 df_train을 사용한다. df_test는 마지막에 모델을 평가할 때 사용한다.
모델 설정하기
sklearn의 tree.DecisionTreeClassifier() 클래스를 이용하면 의사결정나무 모델을 만들 수 있다. 먼저 모델을 만드는 데 사용할 clf를 만들자. tree.DecisionTreeClassifier()에는 다음과 같은 파라미터를 입력한다.
-
random_state: 난수 초깃값. 변수 선택 과정에서 난수를 이용하기 때문에 코드를 실행할 때마다 결과가 조금씩 달라진다. 난수를 고정하면 코드를 여러 번 실행해도 결과가 항상 같다.
-
max_depth: 나무의 깊이. 노드를 최대 몇 번까지 분할할지 정한다. 숫자가 클수록 노드를 여러 번 분할해 복잡한 모델을 만든다. 값을 지정하지 않으면 노드를 최대한 많이 분할한다. 여기서는 단순한 모델을 만들도록 3을 입력하겠다.
from sklearn import tree
clf = tree.DecisionTreeClassifier(random_state=1234, # 난수 고정
max_depth=3) # 나무 깊이
clf는 classifier의 줄임말이다. 고소득/저소득처럼 데이터를 몇 개 중 하나로 분류하는 모델을 분류 모델(classification model) 또는 분류기(classifier)라 한다.
모델 만들기
앞에서 만든 clf를 이용해 모델을 만들어보자. 먼저 df_train에서 에측 변수와 타겟 변수를 각각 추출해 데이터프레임을 만든다. 그런 다음 clf.fit()의 X에는 예측 변수, y에는 타겟 변수를 입력한다.
train_x = df_train.drop(columns='income') # 예측 변수 추출
train_y = df_train['income'] # 타겟 변수 추출
model = clf.fit(X=train_x, y=train_y) # 모델 만들기
model
DecisionTreeClassifier(max_depth=3, random_state=1234)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
DecisionTreeClassifier(max_depth=3, random_state=1234)
모델을 만들 때 난수를 고정하는 이유
의사결정나무 알고리즘은 타겟 변수를 가장 잘 분리해 주는 예측 변수를 선택해 노드를 분할한다. 그런데 여러 예측 변수가 똑같이 타겟 변수를 잘 분리해내는 경우가 있다. 이럴 때 난수를 이용해 무작위로 예측 변수를 선택하기 때문에 코드를 실행할 때마다 결과가 조금씩 달라진다. 코드를 여러 번 실행해도 항상 같은 결과가 나오게 하려면 난수를 고정해야 한다.
모델 구조 살펴보기
완성된 모델을 그래프로 만들어 구조를 살펴보겠다. tree.plot_tree()을 이용하면 모델을 시각화할 수 있다. 먼저 그래프를 크고 선명하게 표현하도록 설정한 다음 그래프를 출력하겠다.
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize': [12, 8], # 그래프 크기 설정
'figure.dpi': '100'}) # 해상도 설정
tree.plot_tree(model); # 그래프 출력
tree.plot_tree()에 몇 가지 파라미터를 추가해 그래프를 보기 좋게 수정하겠다.
tree.plot_tree(model,
feature_names=train_x.columns, # 예측 변수명
class_names=["high", "low"], # 타겟 변수 클래스, 알파벳순
proportion=True, # 비율 표기
filled=True, # 색칠
rounded=True, # 둥근 테두리
impurity=False, # 불순도 표시
label='root', # label 표시 위치
fontsize=10); # 글자 크기
노드의 값
그래프에서 가장 위에 있는 첫 번째 노드를 이용해 그래프를 해석하는 방법을 알아보자. 다른 노드도 같은 순서로 값이 표현되어 있다.

- 전체 데이터의 몇 퍼센트가 해당 노드로 분류됐는지 나타낸다. 첫 번째 노드는 아직 한 번도 나뉘지 않았으므로 데이터의 100%가 이 노드에 속한다.
다음 단계의 노드로 내려가면 데이터가 여러 노드로 배분되므로 비율이 줄어든다. 예를 들어 두 번째 단계의 노드를 보면 왼쪽 노드는 54.2%, 오른쪽 노드는 45.8%이다. 같은 단계의 노드 비율을 모두 더하면 100%가 된다.
-
타겟 변수의 클래스별 비율을 알파벳순으로 나타낸다. 타겟 변수 income의 ‘high’와 ‘low’ 중 ‘high’가 알파벳순으로 우선하므로 ‘high’, ‘low’ 순으로 비율이 표시되어 있다. 값을 보면 전체 데이터 중 ‘high’가 23.9%, ‘low’가 76.1%라는 것을 알 수 있다.
-
0.5를 기준으로 타겟 변수의 두 클래스 중 어느 쪽이 더 많은지 나타낸다. ‘high’가 23.9%, ‘low’가 76.1%로 ‘low’가 더 많으므로 ‘low’가 표시된다.
-
노드를 분리할 때 사용할 기준을 나타낸다. 이 기준을 충족하는 데이터는 왼쪽, 충족하지 않는 데이터는 오른쪽 노드로 할당된다.
marital_status_Married-civ-spouse는 원핫 인코딩으로 만들어진 변수로 기혼이면 1, 비혼이면 0으로 되어 있다. 따라서 비혼이면 변수의 값이 0이므로 ‘marital_status_Married-civ-spouse <= 0.5(비혼)’ 조건을 충족해 왼쪽 노드로 내려가고, 기혼이면 조건을 충족하지 않으므로 오른쪽 노드로 내려간다. 즉, 비혼은 왼쪽 노드, 기혼은 오른쪽 노드로 내려간다.
다른 노드도 분리 기준이 표시되지만 마지막 단계의 ‘끝 노드’는 더 이상 나뉘지 않으므로 분리 기준이 표시되지 않는다.
첫 번째 단계의 노드를 뿌리 노드(root node), 마지막 단계의 노드를 끝 노드(terminal node)라 한다. 어떤 노드의 윗 단계에 있는 노드를 부모 노드(parent node), 아랫 단계에 있는 노드를 자식 노드(child node)라 한다.
왼쪽 노드
이번에는 첫 번째 노드의 조건에 따라 나뉘어진 두 번째 단계의 노드를 해석해보겠다. 먼저 왼쪽 노드를 살펴보자.
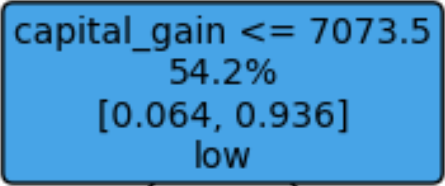
첫 번째 노드의 조건 ‘marital_status_Married-civ-spouse <= 0.5(비혼)’을 충족한 비혼자가 이 노드에 할당된다. 비혼자는 전체의 54.2%이다. 비혼자의 income은 ‘high’ 6.4%, ‘low’ 93.6%로 ‘low’가 더 많다. 다음으로 노드를 나누는 기준은 ‘capital_gain <= 7037.5’이다.
오른쪽 노드

첫 번째 노드의 조건 ‘marital_status_Married-civ-spouse <= 0.5(비혼)’을 충족하지 않은 기혼자가 이 노드에 할당된다. 기혼자는 전체의 45.8%이다. 기혼자의 income은 ‘high’ 44.7%, ‘low’ 55.3%로 ‘low’가 더 많다. 다음으로 노드를 나누는 기준은 ‘education_num <= 12.5’이다.
노드의 색
-
노드의 색깔은 우세한 타겟 변수의 클래스에 따라 정해진다. 그래프를 보면 ‘high’의 비율이 높은 노드는 주황색, ‘low’의 비율이 높은 노드는 파란색 계열로 표현되어 있다.
-
노드의 색농도는 ‘한 클래스의 구성 비율이 우세한 정도’를 나타낸다. 한 클래스의 비율이 다른 클래스보다 높을수록 농도가 진하고, 두 클래스의 비율이 비슷할수록 농도가 연하다. 두 번째 단계의 노드를 보면 왼쪽 노드는 ‘high’보다 ‘low’의 비율이 월등히 높아 농도가 진한 반면, 오른쪽 노드는 두 클래스의 비율이 비슷하므로 농도가 연하다. ‘한 클래스의 비율이 우세한 정도’를 순도(purity)라 한다.
모델을 이용해 예측하기
앞에서 만든 모델을 활용해 새 데이터의 타겟 변수를 예측하는 방법을 알아보겠다. 먼저 모델을 만들 때 사용하지 않은 df_test에서 예측 변수와 타겟 변수를 각각 추출한다.
test_x = df_test.drop(columns='income') # 예측 변수 추출
test_y = df_test['income'] # 타겟 변수 추출
model.predict()를 이용하면 모델을 이용해 새 데이터의 타겟 변수 값을 예측할 수 있다. model.predict()에 test_x를 입력해 타겟 변수 예측값을 구한 다음 df_test[‘pred’]에 할당한다. df_test를 출력하면 가장 오른쪽에 pred가 만들어진 것을 확인할 수 있다. pred는 모델이 train_x에 들어 있는 예측 변수만 이용해서 구한 값이다.
# 예측값 구하기
df_test['pred'] = model.predict(test_x)
df_test
| age | education_num | capital_gain | capital_loss | hours_per_week | workclass_? | workclass_Federal-gov | workclass_Local-gov | workclass_Never-worked | workclass_Private | ... | native_country_Scotland | native_country_South | native_country_Taiwan | native_country_Thailand | native_country_Trinadad&Tobago | native_country_United-States | native_country_Vietnam | native_country_Yugoslavia | income | pred | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11712 | 58 | 10 | 0 | 0 | 60 | 0 | 0 | 0 | 0 | 0 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | low | low |
| 24768 | 39 | 10 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | low | low |
| 26758 | 31 | 4 | 0 | 0 | 20 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | low | low |
| 14295 | 23 | 9 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | low | low |
| 3683 | 24 | 9 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | low | low |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 11985 | 24 | 13 | 0 | 0 | 30 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | low | low |
| 48445 | 35 | 13 | 10520 | 0 | 45 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | high | high |
| 19639 | 41 | 9 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | high | low |
| 21606 | 29 | 4 | 0 | 0 | 30 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | low | low |
| 3822 | 31 | 13 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 1 | ... | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | low | low |
14653 rows × 109 columns
income과 pred의 값을 보면 모델의 에측이 맞았는지 알 수 있다. 두 변수의 값이 같으면 예측이 맞은 것이고, 두 변수의 값이 다르면 예측이 틀린 것이다.
성능 평가하기
예측값을 실제값과 대조해 에측이 얼마나 잘 맞았는지 모델의 성능을 평가하겠다. 성능 평가 지표는 종류가 다양하고 특징이 서로 달라서 어떤 지표가 높더라도 다른 지표는 낮을 수 있다. 그러므로 모델을 사용하는 목적에 맞게 평가 기준으로 삼을 지표를 선택해야 한다.
confusion matrix 만들기
모델이 예측한 값 중 맞은 경우와 틀린 경우의 빈도를 나타낸 컨퓨전 매트릭스(confusion matrix, 혼동 행렬)를 만들겠다. sklearn.metrics의 confusion_matrix()를 이용하면 컨퓨전 매트릭스를 만들 수 있다. confusion_matrix()에는 다음 파라미터를 입력한다.
-
y_true: 타겟값
-
y_pred: 예측값
-
labels: 클래스 배치 순서
from sklearn.metrics import confusion_matrix
conf_mat = confusion_matrix(y_true=df_test['income'], # 실제값
y_pred=df_test['pred'], # 예측값
labels=['high', 'low']) # 클래스 배치 순서
conf_mat
array([[ 1801, 1705],
[ 582, 10565]], dtype=int64)
sklearn.metrics의 ConfusionMatrixDisplay()를 이용해 컨퓨전 매트릭스로 히트맵heatmap을 만들어 값을 살펴보겠다. 히트맵은 격자 위에 값을 표시하고 값이 클수록 셀의 색농도를 진하게 표현한 그래프다.
plt.rcParams.update(plt.rcParamsDefault) # 그래프 설정 되돌리기
from sklearn.metrics import ConfusionMatrixDisplay
p = ConfusionMatrixDisplay(confusion_matrix=conf_mat, # 컨퓨전 매트릭스
display_labels=('high', 'low')) # 타겟 변수 클래스명
p.plot(cmap='Blues'); # 컬러맵 적용해 출력
confusion matrix 해석하기
컨퓨전 매트릭스의 행은 실제true 빈도를 의미한다. 첫 번째 행은 income이 실제로 high인 사람, 두 번째 행은 실제로 low인 사람을 나타낸다.
열은 모델이 예측한predicted빈도를 의미한다. 첫 번째 열은 모델이 high로 예측한 사람, 두 번째 열은 low로 예측한 사람을 나타낸다.
컨퓨전 매트릭스를 보면 예측이 맞은 빈도와 틀린 빈도를 알 수 있다. 행과 열의 레이블label이 같은 왼쪽 대각선의 두 셀은 예측이 맞은 빈도를 나타낸다. 반대로 레이블이 서로 다른 오른쪽 대각선의 두 셀은 예측이 틀린 빈도를 나타낸다. 앞에서 출력한 컨퓨전 매트릭스를 보면 다음과 같은 사실을 알 수 있다.
첫 번째 열의 값
-
모델이 2,383(1,801 + 582)을 high로 예측했다.
-
이 중 실제로 high인 사람은 1,801명이다(정답).
-
이 중 실제로 low인 사람은 582명이다(오답).
두 번째 열의 값
-
모델이 12,270(1,705 + 10,565)을 low로 예측했다.
-
이 중 실제로 low인 사람은 10,565명이다(정답).
-
이 중 실제로 high인 사람은 1,705명이다(오답).
컨퓨전 매트릭스의 셀 이름
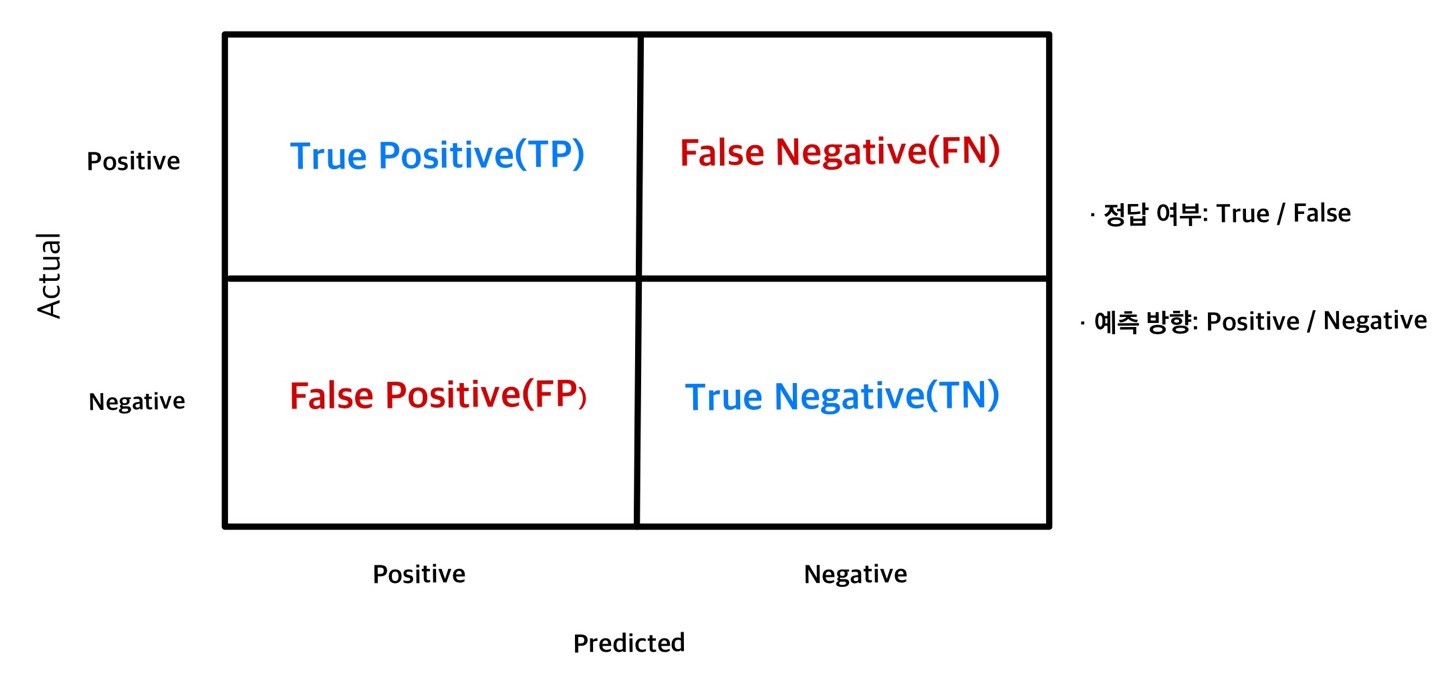
컨퓨전 매트릭스의 각 셀은 다음과 같은 단어로 표현한다.
-
정답 여부(True/False): 모델의 예측값이 실제값과 일치하면 True, 일치하지 않으면 False
-
예측 클래스(Positive/Negative): 타겟 변수의 클래스 중 모델이 예측하고자 하는 관심 클래스는 Positive, 그 반대는 Negative. 여기서는 모델의 목적이 고소득자를 찾아내는 것이므로 income이 high면 Positive, low면 Negative가 된다.
컨퓨전 매트릭스의 셀 이름은 True/False와 Positive/Negative의 첫 글자를 따서 TP, TN, FP, FN으로 줄여서 표현할 때가 많다. 줄임말을 알아 두면 성능 지표 공식을 이해하기 편하다.
성능 평가 지표 구하기
성능 평가 지표를 구하면 모델의 예측이 얼마나 정확한지 알 수 있다.
Accuracy
accuracy(정확도)는 모델이 ‘예측해서 맞춘 비율’을 의미한다. 컨퓨전 매트릭스 전체 셀 합계에서 왼쪽 대각선 셀의 합계가 차지하는 비율이 accuracy이다. 모델의 성능을 평가할 때 기본적으로 accuracy를 가장 먼저 구한다.
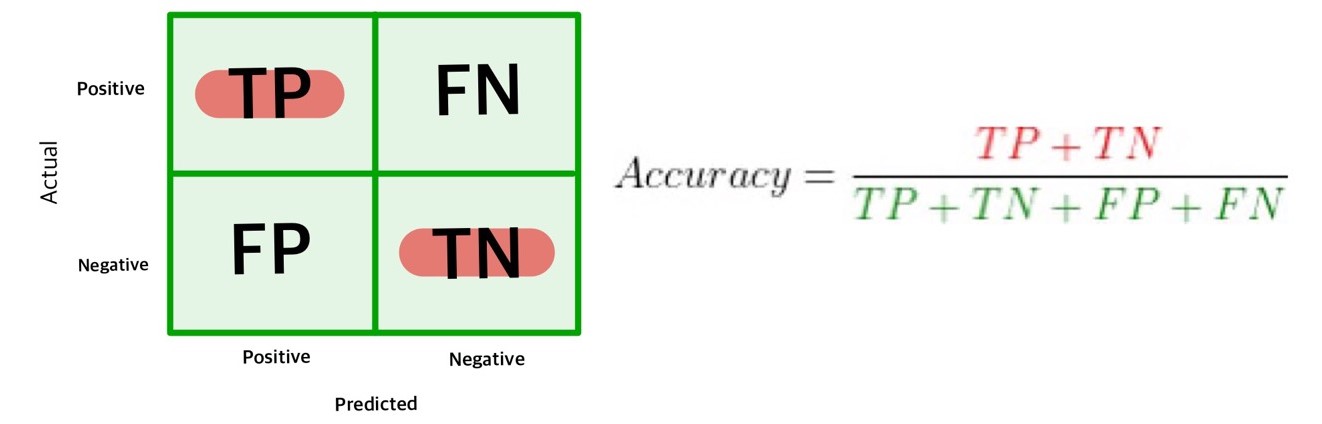
accuracy는 앞에서 만든 conf_mat을 이용해 직접 계산할 수도 있지만 sklearn.metrics의 accuracy_score()를 이용하면 구할 수 있다. 다음 코드의 출력 결과를 보면 accuracy가 약 84.3%라는 것을 알 수 있다.
import sklearn.metrics as metrics
metrics.accuracy_score(y_true=df_test['income'], # 실제값
y_pred=df_test['pred']) # 예측값
0.8439227461953184
accuracy는 타겟 변수의 클래스별 비율이 불균형하면 신뢰하기 어렵다는 제한점이 있다. 이 장에서 사용한 adult 데이터는 연소득이 low에 해당하는 사람이 76%로 매우 많다. 그러므로 어떤 데이터를 입력하든 항상 low로 예측하는 이상한 모델을 만들더라도 accuracy는 최소 76%가 된다. 따라서 accuracy만 봐서는 점수가 높더라도 모델의 성능이 좋아서인지 아니면 자료가 불균형해서인지 판단할 수 업다.
Precision
precision(정밀도)은 모델이 ‘관심 클래스를 예측해서 맞춘 비율’을 의미한다. 고소득자 예측 모델에서는 모델이 income을 high로 예측한 사람 중에서 실제로 high인 사람의 비율이 precision이다. 다른 예로 당뇨병 예측 모델이라면 모델이 발병으로 예측한 사람 중에서 실제 발병한 사람의 비율이 precision이다. 컨퓨전 매트릭스 첫 번재 열의 셀 합계에서 위쪽 셀이 차지하는 비율을 구하면 precision이 된다.
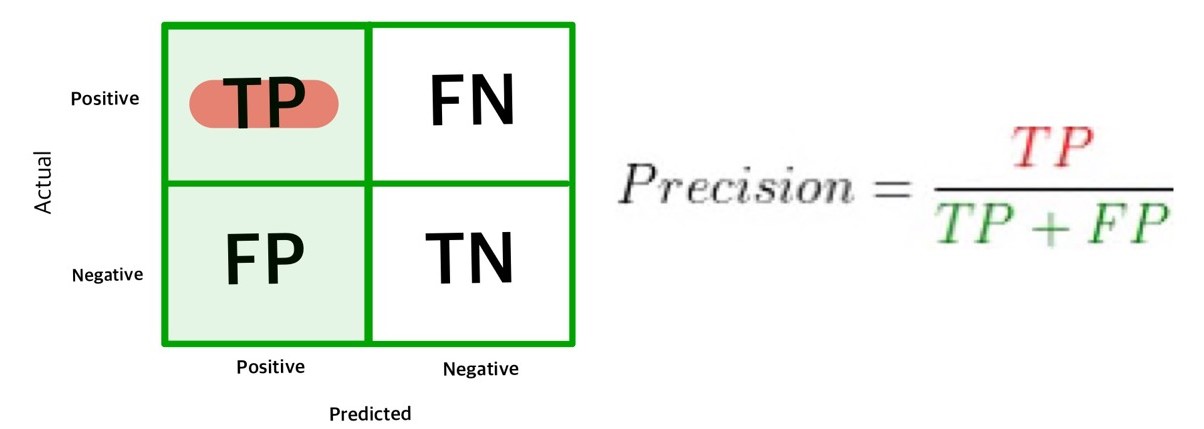
metrics.precision_score()를 이용하면 precision을 구할 수 있다. 다음 코드의 출력 결과를 보면 모델의 precision이 75.5%이다. 따라서 모델이 income을 high로 예측한 사람 중 75.5%가 실제로 high이고, 나머지 24.5%는 실제로는 low인데 high로 잘못 분류한 것이다.
metrics.precision_score(y_true=df_test['income'], # 실제값
y_pred=df_test['pred'], # 예측값
pos_label='high') # 관심 클래스
0.7557700377675199
Recall
recall(재현율)은 모델이 ‘실제 데이터에서 관심 클래스를 찾아낸 비율’을 의미한다. 고소득자 예측 모델에서는 income이 실제로 high인 사람 중에서 모델이 high로 예측해서 찾아낸 사람의 비율이 recall이다. 다른 예로 당뇨병 예측 모델이라면 실제 당뇨병 발병자 중에서 모델이 발병으로 예측해서 찾아낸 비율이 recall이다. 컨퓨전 매트릭스 첫 번째 행의 셀 합계에서 왼쪽 셀이 차지하는 비율을 구하면 recall이 된다.
recall과 precision은 계산할 때 분모에 놓는 값이 다르다. precision은 모델이 ‘관심 클래스로 예측한 빈도’를 분모에 놓고 구하는 반면, recall은 ‘실제 관심 클래스의 빈도’를 분모에 놓고 구한다.
sensitivity(민감도)도 recall과 같은 의미로 쓰인다.
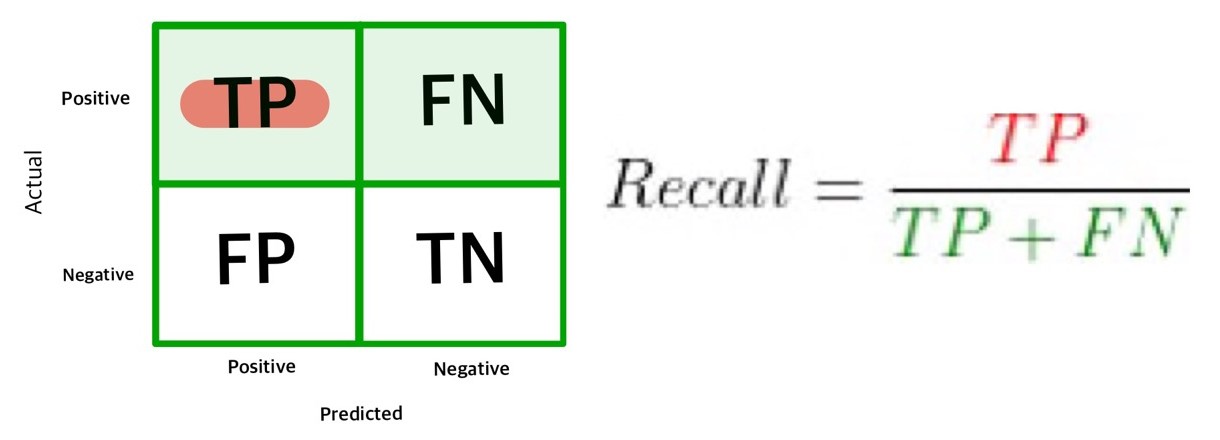
metrics.recall_score()를 이용하면 recall을 구할 수 있다. 다음 코드의 출력 결과를 보면 모델의 recall이 51.3%이다. 따라서 실제로 income이 high인 사람 중에서 51.3%를 모델이 high로 맞게 예측해서 찾아냈고, 나머지 48.7%는 low로 잘못 예측해서 놓친 것이다.
metrics.recall_score(y_true=df_test['income'], # 실제값
y_pred=df_test['pred'], # 예측값
pos_label='high') # 관심 클래스
0.5136908157444381
F1 score
recall과 precision이 모두 중요할 때는 recall과 precision의 크기를 함께 반영한 F1 score를 사용한다. F1 score는 recall과 precision의 조화평균으로, 0 ~ 1 사이의 값을 지니며 성능이 높을수록 1에 가까운 값이 된다. recall과 precision을 곱해서 구하기 때문에 둘 중 하나라도 0이면 0이 된다.
F1 score는 F-score, F-measure라고도 한다.
F1 score는 accuracy와 달리 타겟 변수의 클래스가 불균형해도 모델의 성능을 잘 표현한다. 예를 들어 Negative 클래스가 훨씬 많은 불균형 데이터를 예측할 때 어떤 모델은 데이터를 대부분 Negative로만 예측하고 Positive로는 거의 예측하지 않을 수 있다. 이런 모델은 Positive 클래스를 거의 맞추지 못해 recall과 precision이 낮은데도 accuracy를 구하면 매우 높게 나온다. 반면 F1 score는 recall과 precision의 조화평균이기 때문에 매우 낮게 나온다.
F1 score는 recall과 precision을 고루 반영하고 클래스가 불균형해도 모델의 성능을 잘 나타내므로 여러 모델의 성능을 한가지 지표로 비교해야 할 때 특히 자주 사용된다.
metrics.f1_score()를 이용하면 F1 score를 구할 수 있다. 다음 코드의 출력 결과를 보면 모델의 F1 score가 0.61이다.
metrics.f1_score(y_true=df_test['income'], # 실제값
y_pred=df_test['pred'], # 예측값
pos_label='high') # 관심 클래스
0.6116488368143997
어떤 성능 평가 지표를 사용해야 할까?
성능 평가 지표는 특징이 서로 달라서 어떤 지표가 높더라도 다른 지표는 낮을 수 있다. 그러므로 모델을 사용하는 목적에 맞게 평가 기준으로 삼을 지표를 선택해야 한다. accuracy는 모델의 일반적인 성능을 나타내므로 항상 살펴봐야 하고, 이에 더해 목적에 따라 precision 또는 recall 중 한 가지 이상을 함께 살펴봐야 한다.
precision: 관심 클래스가 분명할 때
모델을 사용하는 목적이 타겟 변수의 클래스 중에서 관심을 두는 한쪽 클래스를 정확하게 예측하는 것이라면 precision 기준으로 성능을 평가해야 한다. 예를 들어 고소득자를 예측해 고가의 제품을 홍보한다면 모델이 고소득자로 예측했을 때 얼마나 잘 맞는지 살펴봐야 하므로 precision을 기준으로 평가해야 한다. 이처럼 타겟 변수의 한쪽 클래스에 분명한 관심이 있을 때 precision을 사용한다.
recall: 관심 클래스를 최대한 많이 찾아내야 할 때
모델을 사용하는 목적이 관심 클래스를 최대한 많이 찾아내는 것이라면 recall 기준으로 성능을 평가해야 한다. 예를 들어 전염병에 감염된 사람을 최대한 많이 찾아내 격리해야 한다면, 실제로 전염병에 감염된 사람 중에서 몇 퍼센트를 감염된 것으로 에측하는지 살펴봐야 하므로 recall을 기준으로 평가해야 한다.
관심 클래스로 예측해서 틀릴 때 손실 VS 관심 클래스를 놓칠 때 손실
평가 기준으로 삼을 지표를 결정하는 또 다른 방법은 데이터를 ‘관심 클래스로 예측해서 틀릴 때’의 손실과 ‘관심 클래스를 놓칠 때’의 손실 중 무엇이 더 큰지를 놓고 판단하는 것이다. 데이터를 관심 클래스로 예측해서 틀릴 때의 손실이 더 크면 precision, 반대로 관심 클래스를 놓칠 때 손실이 더 크면 recall을 평가 기준으로 사용하면 된다.
예시 1) 고소득자에게 값비싼 선물을 보내 구매를 독려하는 마케팅 활동
-
관심 클래스로 예측해서 틀릴 때의 손실: 구매할 가능성이 낮은 저소득자에게 값비싼 선물을 보냄
-
관심 클래스를 놓칠 때의 손실: 구매할 가능성이 있는 고소득자에게 선물을 보내지 않음
이때는 데이터를 관심 클래스로 예측해서 틀릴 때의 손실이 더 크다. 따라서 비관심 클래스negative를 관심 클래스positive로 예측하는 오류(false positive)를 줄여야 하므로 precision 기준으로 모델을 평가해야 한다.
예시 2) 전염병에 걸린 사람을 찾아 격리하는 방역 활동
-
관심 클래스로 예측해서 틀릴 때의 손실: 정상인을 확진자로 분류해서 불필요하게 격리함
-
관심 클래스를 놓칠 때의 손실: 확진자를 격리하지 않아서 전염병이 확산됨
이때는 관심 클래스를 놓칠 때의 손실이 더 크다. 따라서 관심 클래스positive를 비관심 클래스negative로 예측하는 오류(false negative)를 줄여야 하므로 recall 기준으로 모델을 평가해야 한다.
비관심 클래스(Negative)를 관심 클래스(Positive)로 잘못 예측하는 False Positive를 1종 오류(Type 1 error) 또는 알파 오류(α error)라 한다. 반대로 관심 클래스(Positive)를 비관심 클래스(Negative)로 잘못 예측하는 False Negative를 2종 오류(Type 2 error) 또는 베타 오류(β error)라 한다.
F1 score: recall과 precision이 모두 중요할 때
데이터를 관심 클래스로 예측해서 틀릴 때의 손실과 관심 클래스를 놓칠 때의 손실이 둘 다 중요하다면 recall과 precision을 모두 판단 기준으로 삼아야 한다. 그런데 여러 모델을 만들어 성능을 비교할 때 평가 기준 지표가 여러 개면 지표에 따라 성능이 좋다고 판단되는 모델이 다를 수 있다. 이럴 때는 F1 score를 평가 기준으로 삼으면 된다. F1 score를 이용하면 여러 모델 중에 어떤 모델이 우수한지 한 가지 기준으로 비교할 수 있다.
모델의 성능 지표가 얼마면 될까?
모델의 성능 지표는 얼마를 넘겨야 모델을 사용할 수 있다는 절대적인 기준이 없다. 모델이 쓸만한지는 기존에 해오던 방식으로 예측했을 때와 모델을 이용해 예측했을 때의 성능 지표를 비교해야 한단할 수 있다. 예를 들어 모델의 accuracy가 60%밖에 안 된다고 하더라도 기존 방식으로 사람이 직접 예측했을 때 accuracy가 55%라면 모델을 사용하는 게 낫다고 판단할 수 있다. 반대로 모델의 accuracy가 95%로 높더라도 기존 방식의 accuracy가 96%라면 기존 방식을 유지하는 게 낫다고 판단할 수 있다.
예측 방식을 선택할 때는 예측에 드는 시간과 비용도 고려해야 한다. 예측 성능이 아무리 좋더라도 예측하는 데 시간이 너무 오래 걸리고 비용이 많이 든다면 사용하기 어렵다. 따라서 모델을 이용해 예측할 때와 기존 방식으로 예측할 때 드는 시간과 비용을 비교해 모델을 사용할지 여부를 결정해야 한다.
F1 score를 구할 때 왜 조화평균을 사용할까?
조화평균은 ‘역수의 산술평균의 역수’이다.주어진 수들의 역수를 구해 산술평균을 구한 다음 다시 역수를 구하면 조화평균이 된다.
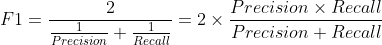
F1 score를 구할 때 주어진 수들의 합을 수의 개수로 나누는 산술평균이 아니라 조화평균을 이용하는 이유는 recall과 precision 중 하나라도 작으면 값을 크게 낮추기 위해서다. 예를 들어 recall이 99%, precision이 1%일 때 산술평균을 구하면 50%지만, 조화평균을 구하면 1.98%이다.
-
산술평균: (0.99 + 0.01) / 2 = 0.5
-
조화평균: 2 * (0.99 * 0.01) / (0.99 + 0.01) = 0.0198
댓글남기기